Propuesto por Vicente Vicario García. I.E.S. El Sur, Huelva
Problema 568
Es bien conocido que si un triangulo ABC tiene dos medianas, o dos bisectrices interiores, o dos cevianas Gergonne, o dos simedianas de la misma longitud, entonces el triangulo es necesariamente isósceles. Por otra parte, también es conocido que si un triangulo tiene dos bisectrices exteriores iguales, el triangulo no es necesariamente isósceles. (A este tipo de triángulos se les denomina pseudoisósceles).
Si denominamos antisimediana al segmento conjugado isotomico de la simediana, es decir, el segmento cuyo pie es simétrico del pie de la simediana respecto del punto medio del lado, probar o refutar la siguiente proposición:
“Existen triángulos no isósceles con dos antisimedianas de la misma longitud ”.
Resolución: (Vicente Vicario García, I.E.S. El Sur, Huelva).
A lo largo de la resolución del
problema utilizaremos la notación habitual en la geometría del triangulo, con A, B, C denotando los vértices del mismo; a, b, c las longitudes de los lados; 
, 
, 
, las longitudes de las medianas; 
, 
, 
, las longitudes de las simedianas; y 
, 
, 
las longitudes de las antisimedianas,
respectivamente.
Es bien sabido que si un triangulo tiene dos medianas, o dos bisectores interiores, o dos simedianas, o dos cevianas Gergonne, de la misma longitud, entonces el triangulo es necesariamente isósceles.†
Es
fácil ver que si dos medianas del triangulo tienen la misma longitud 
, entonces
y el triangulo es isósceles. ■
Si
dos bisectrices interiores tienen la misma longitud,
, entonces (teorema de Steiner-Lehmus)
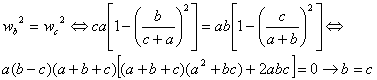
y el triangulo es isósceles. ■
Si dos simedianas tienen la misma longitud, 
, entonces, por la conocida identidad 
, tenemos que(teorema de Lemoine):
y el triangulo es isósceles. ■
Si dos cevianas Gergonne del triangulo son iguales, 
, entonces tenemos que (teorema de K. R.
Sastry):
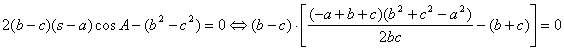
y entonces
y claramente esta igualdad es imposible por la desigualdad triangular, y el triangulo es isósceles. ■
Prueba de la proposición
Estableceremos una proposición no análoga al teorema de Steiner-Lehmus para triángulos con dos antisimedianas de igual longitud. Demostraremos el siguiente teorema de existencia. A el tipo de triángulos como los que especifica la proposición siguiente se los suele denominar triángulos pseudoisósceles.
Teorema: “Existen triángulos no isósceles con dos antisimedianas iguales”.
Demostración: Sea ABC un triangulo. Sean 
, 
, 
, y 
. Entonces, en virtud del teorema de
Steiner para las simedianas
Analogamente
y por el teorema de
los cosenos, y como 
, y 
, entonces
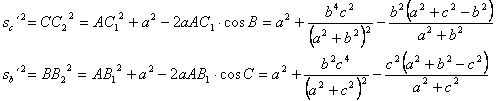
Si
dos antisimedianas de un triangulo tienen la misma longitud,
, entonces, tenemos que
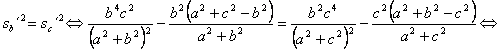
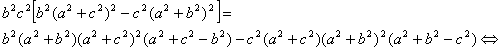
Tenemos, pues, dos casos a considerar
(a) 
y el triangulo es isósceles.
(b) 
. Sin perdida de generalidad,
supondremos que 
. En virtud de la famosa regla de
Descartes para las raíces de una ecuación polinómica, es fácil ver que la
ecuación algebraica tiene exactamente una única raíz real positiva.
Por otra parte, empleando la desigualdad entre las medias aritmética y geométrica,
es fácil ver que 
, y en consecuencia
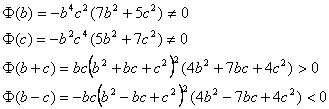
Finalmente,
en virtud del teorema de Bolzano para funciones continuas, tenemos que la única
raíz real positiva 
de la ecuación algebraica satisface 
, y 
, 
, y entonces existe un triangulo no isósceles
con longitudes de sus lados b, c, y
con dos antisimedianas de la misma longitud. Esto completa la demostración.
---oooOooo---
Algunas referencias
[1] Bellot Rosado, F; Triángulos especiales I, II, III. Revista digital OIM de matemáticas.
[2] Sastry, K. R. S; A Gergonne analogue of the Steiner-Lehmus theorem. Forum Geometricorum, Volume 5, (2005), 191-195
[3] Abu-Saymeh, S., Hajja, M., and Ali ShahAli, H.; Another variation on the Steiner-Lehmus theme. Forum Geometricorum, Volume 8, (2008), 131-140.
[4] Hajja, M.; Stronger forms of the Steiner-Lehmus Theorem. Forum Geometricorum, Volume 8, (2008), 157-161.