Problema 569.

04.54 Las alturas de un triángulo ABC se cortan en un punto H. Determínese el valor del ángulo <BCA sabiendo que AB=CH.

De Diego, B.,Llerena, A.,Baena,F.,Rodríguez,M.B.,Gamboa,J.M:,Lorenzo, J.M. (2005): Problemas de Oposiciones. Matemáticas. Oposiciones al Cuerpo de Profesores de Enseñanza Secundaria. p.745 (Ceuta) Año 2004.

Solución del director.

Supongamos que sea ABC el triángulo propuesto.

Es <ABH_b=90º-<BAH_b. Por otra parte, <HCH_b=<H_cCA=90º-<BAC

Por ello, los triángulos rectángulos CHH_b y BAH_b son semejantes.

Al tener además un lado igual, CH=BA, son congruentes.

Así pues, BH_b  = C H_b  

Es decir, que el triángulo BH_bC  es rectángulo isósceles.

Por todo ello, ha de ser <BCA=<BCH_b=45º

Ricardo Barroso Campos

Didáctica de las Matemáticas

Universidad de Sevilla

Una vez preparada esta solución, he recibido del profesor Ricard Peiró y del profesor Ángel Montesdeoca una segunda solución.

Esta es mi versión de la segunda solución.

Si C >90º, H es exterior al triángulo:

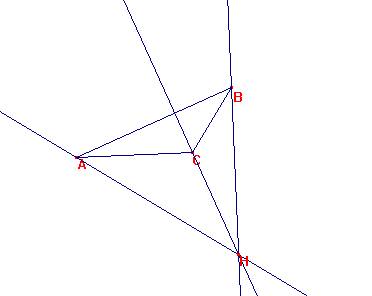
Hagamos la simetría del triángulo y de la altura CH respecto a AB:

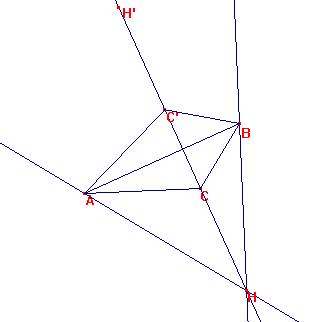
Dado que <HH’B=<BHH’=90º-<ABH=<CAB, H’ pertenece a la circunferencia circunscrita a ABC.

Traslademos paralelamente  C´H´ a B y C, formando la siguiente figura:

UABV es un cuadrado, por ser UA=VB=AB y por perpendicularidad entre UA AB y UB.

Así, es <H’CB=90º-<ABC. <BVH’=90º+<H’VU=90+<C’BA=90º+CBA.

Es decir, H’VBC es un cuadrilátero inscrito, de manera que como H’AC son de la circunscrita a  ABC, V también deber serlo. .

De igual manera, H’UAC es un cuadrilátero inscrito, por lo que haciendo un razonamiento similar, U debe pertenecer a la circunferencia circunscrita.

El cuadrado BVUA es también inscrito en dicha circunferncia.

Las tres circunferencias coinciden, por lo que <AH’B=45º, y por último, <ACB=135º.