Dedicado a Braulio de Diego
Problema 569.- Las alturas de un triángulo
ABC se cortan en un punto H. Determínese el valor del ángulo <BCA sabiendo
que AB=CH.
De Diego, B.,Llerena, A.,Baena,F.,Rodríguez,M.B.,Gamboa,J.M:,Lorenzo, J.M. (2005): Problemas de Oposiciones.
Matemáticas. Oposiciones al Cuerpo de Profesores de Enseñanza Secundaria. p.745
(Ceuta) Año 2004.
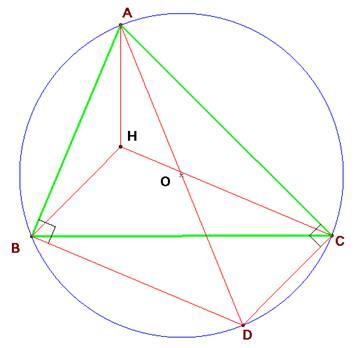 Solución de Saturnino Campo
Ruiz, profesor del I.E.S Fray Luis de León de Salamanca.
Solución de Saturnino Campo
Ruiz, profesor del I.E.S Fray Luis de León de Salamanca.
Con HB y HC como soporte construyo el paralelogramo HBDC. Como BD es paralelo a HC, resulta ser ortogonal a AB. Por lo mismo CD es ortogonal a AC y por tanto, el cuadrilátero ABDC es cíclico o inscriptible. El ángulo BCA es igual al ángulo BDA, que mide 45º, ya que AB=CH (por hipótesis) = BD y ABD es rectángulo en B.