Problema 570
Sea ABC un triángulo escaleno en el que una
altura, una bisectriz interior y una mediana (cada una de las cevianas
anteriores parten de un vértice distinto) son iguales. Supongamos, sin pérdida
de generalidad, que ![]() . Demostrar que las longitudes de los lados del
triángulo ABC cumplen la siguiente
relación:
. Demostrar que las longitudes de los lados del
triángulo ABC cumplen la siguiente
relación:
![]()
Resolución: Vicente Vicario García, I.E.S. El Sur, Huelva
A lo largo de la resolución del problema emplearemos la notación habitual en la geometría del triángulo. Comenzaremos con un lema clásico que necesitamos.
Lema: “Si ABC es un triángulo arbitrario entonces se cumple que:
![]() y
y ![]() ”.
”.
Demostración: Se basa en aplicar el teorema de los cosenos al triángulo ABC y en las siguientes expresiones con sus simplificaciones
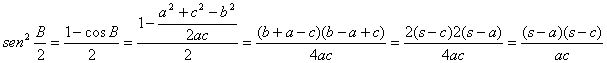
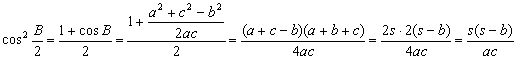
lo que concluye la demostración del lema. ■
Nos
centramos ahora en el problema y partimos de una conocida expresión para la
bisectriz interior. De esta forma, a partir de la igualdad ![]() deducimos
deducimos
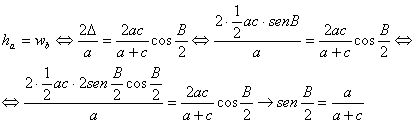
Por otra parte, de la igualdad ![]() , a partir de una conocida expresión para la mediana,
utilizando el lema y la expresión deducida para senB/2 anteriores, tenemos
, a partir de una conocida expresión para la mediana,
utilizando el lema y la expresión deducida para senB/2 anteriores, tenemos
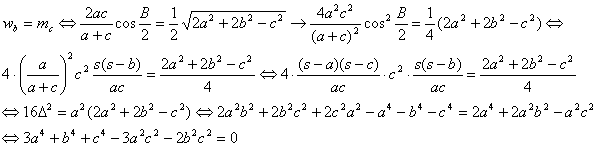
donde la última igualdad es una condición que cumplen las longitudes de los lados del triángulo que estamos estudiando. Lo que concluye la demostración.
---oooOooo---