Problema 571.- (Propuesto por J. B. Romero Márquez,
profesor colaborador de
Sean ABC, con a como hipotenusa y b, c como catetos, un triangulo rectángulo.
Sean también A B´ C´ con a´ como hipotenusa, y b´, c´
como catetos, otro triangulo rectángulo, cuyas alturas desde A y A´
son 
y 
, respectivamente. Sean m,
n, m´, n´ las proyecciones
ortogonales sobre la hipotenusa a, a´, de los catetos b, c y b´, c´
respectivamente. Probar que:
(a) 
¿Cuándo se alcanza
la igualdad?
(b) 
¿Cuándo se alcanza
la igualdad?
Romero, J.B.(2010): Comunicación personal.
Resolución: (Vicente Vicario García, I.E.S. El Sur,
Huelva)
(a) Es claro que
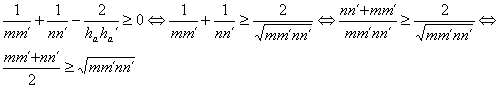
y esta ultima desigualdad es inmediata en virtud de la desigualdad entre las medias aritmética y geométrica, alcanzándose la igualdad si y solo si
(b) también es claro que
(c)
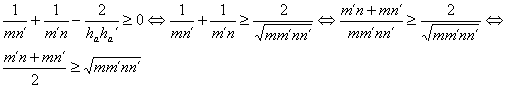
y, de nuevo esta desigualdad es inmediata en virtud de la desigualdad entre las medias aritmética y geometria, alcanzándose la igualdad si y solo si
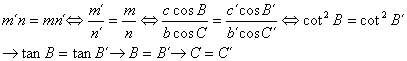
---oooOooo---