Problema 572

Construir sobre los lados BC, CA, AB de un triángulo ABC, exteriormente, los cuadrados BCDE, ACFG, BAHK, y construir los paralelogramos  FCDQ, EBKP. Demostrar que APQ es un triángulo rectángulo isósceles.
Demir, H (1968)American Mathematical Monthly, Vol 75 p 899 problem E2124. Propuesto por Hüseyin Demir; Midle East Technical University, Ankara, Turkey

Solución del director:

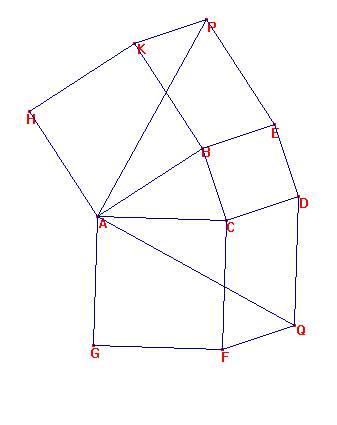
Consideremos el paralelogramo HKPR y su diagonal HP. También consideremos los segmentos CQ y BQ:

Es HR=KP=BE=BC,   HR paralelo a KH, paralelo a BE, y perpendicular a BC

AH=AC, AH perpendicular a AB.

Luego <RHA=<CBA, y por tanto es AR=AC y ambos son perpendiculares.

El triángulo ARP tiene, pues: AR=AC, RP=HK=AB,

<ARP= 360º -<HRA-<HRP= 360º - C  -   90º – B=90º+A

Así un giro de 90º  y centro A transforma AHR en ABC.

 Por otra  parte, en el triángulo ACQ tenemos :

  CF=CA, FQ=CD=CB, <CFD=180º-FCD=180º-(180º-C)=C. Es decir que CQ=AB, <FCQ=A.

Además, ACQ=90º+A, por lo que los triángulos ARP y ACQ son iguales. Así AR=AQ.

Además un giro de 90º y centro en A transforma ARP en ACQ, cqd.

 Ricardo Barroso Campos

Didáctica de las Matemáticas

Universidad de Sevilla