Problema 572.- Construir sobre los lados BC, CA, AB de un triángulo ABC, exteriormente, los cuadrados BCDE, ACFG, BAHK, y construir los paralelogramos FCDQ, EBKP. Demostrar que APQ es un triángulo rectángulo isósceles.
Demir, H ()American Mathematical Monthly(1968), Vol 75 p 899 problem E2124. Propuesto por Hüseyin Demir; Midle East Technical University, Ankara, Turkey
Solución de Saturnino Campo Ruiz, profesor del I.E.S Fray Luis de León de Salamanca.
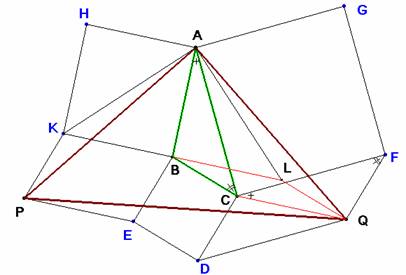 Comenzamos demostrando que los triángulos CQF y ABC son congruentes y de lados perpendiculares. En efecto, el ángulo en F del primero es igual al ángulo en C del segundo y los lados homólogos son iguales. De esto se sigue que CQ es perpendicular a AB, e igual a él. Construimos ahora el paralelogramo BCQL. AB es la mediatriz de KL. El triángulo AKL es rectángulo en A e isósceles. Por tanto, un giro de 90º y centro A transforma el triángulo AKP en el triángulo ALQ, y con esto queda demostrado que APQ es rectángulo en A e isósceles.
Comenzamos demostrando que los triángulos CQF y ABC son congruentes y de lados perpendiculares. En efecto, el ángulo en F del primero es igual al ángulo en C del segundo y los lados homólogos son iguales. De esto se sigue que CQ es perpendicular a AB, e igual a él. Construimos ahora el paralelogramo BCQL. AB es la mediatriz de KL. El triángulo AKL es rectángulo en A e isósceles. Por tanto, un giro de 90º y centro A transforma el triángulo AKP en el triángulo ALQ, y con esto queda demostrado que APQ es rectángulo en A e isósceles.