Propuesto por Vicente Vicario García, I.E.S. El Sur,
Huelva
Problema 573.-
Sea ABC un triángulo
acutángulo. Consideremos las cevianas que partiendo desde cada vértice del
mismo pasan por su circuncentro. Sean D,
E, F los pies de estas cevianas respecto de los lados BC, AC
y AB del triángulo, respectivamente. (a)
Demostrar que al menos uno de los segmentos OD,
OE, OF es mayor o igual que el radio de la circunferencia inscrita al
triángulo.
(b) Demostrar que se puede
refinar el apartado anterior y garantizar que al menos uno de los segmentos OD, OE,
OF anteriores, es mayor o igual que
la mitad del radio de la circunferencia circunscrita al triángulo.
Nota: Evidentemente, a partir
de la desigualdad de Euler-Chapple 
, el apartado (a) se deduce como corolario del apartado (b)
que es un resultado más fuerte. Por otra parte, se puede intentar demostrar (a)
sin demostrar primero (b).
Vicario, V. (2010): Comunicación personal.
Resolución: (Vicente Vicario García, I.E.S. El Sur,
Huelva)
(a) A lo largo de la resolución del problema
utilizaremos la notación habitual en la geometría del triángulo. Puesto que el
triángulo es acutángulo, el circuncentro es interior al mismo. Emplearemos el
famoso teorema de Carnot, que afirma que la suma de las distancias del
circuncentro de un triángulo acutángulo a sus lados es 
. De esta forma, si denotamos por M, N, P los puntos medios respectivos de los
lados BC, AC y AB del triángulo, se
deduce inmediatamente que
por lo que, al
menos uno, de los segmentos OD, OE, OF
(digamos OF) debe medir una longitud
mayor o igual que
. Finalmente, utilizando la desigualdad de Euler-Chapple , es inmediato obtener el resultado
lo que concluye la primera parte. Observemos que esta demostración es independiente de la que daremos en el apartado siguiente.
(b) Para este apartado necesitamos dos lemas.
Los dos lemas, curiosamente, aparecen en el artículo “Algunas aplicaciones de la noción de área: El triángulo de Routh y los triángulos
cevianos” de D. Francisco Bellot del numero 15 de la revista digital de
Lema 1: “Entre todos los triángulos cevianos, el de mayor área es el triángulo medial cuya área es la cuarta parte del triángulo original”.
Demostración: Viene presente en el artículo ya comentado. ■
Lema 2: “Sea 
el área de un triángulo.
Entonces el área de su triángulo ceviano respecto del circuncentro viene dado
por
”.
Demostración:
Proponemos una demostración (ya que no aparece en el citado artículo, aunque el
resultado final aparece explícitamente). De nuevo, indicamos que por ser acutángulo
el triángulo, su circuncentro es interior al mismo. Sean 
y 
la altura y la
circuntriz desde el vértice A (pasa a
través del circuncentro) del triángulo, respectivamente Es bien conocido que
estas líneas son isogonales, con lo que es inmediato observar que el ángulo que
forman es 
, y en consecuencia, 
.
Con la notación inicial, basta aplicar relaciones de semejanza para obtener
y análogamente para los segmentos OE y OF. De esta forma
Por otra parte, es inmediato
comprobar que a partir de lo comentado anteriormente, tenemos que 
, 
, etc. De esta forma, podemos expresar el área del triangulo
ceviano DEF por las expresiones
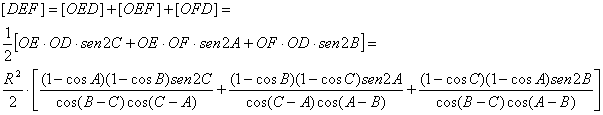
Después de un calculo laborioso, pero sencillo, se llega finalmente a la expresión correspondiente para el área del triangulo ceviano que buscamos
■
Centrándonos ahora en el problema, (utilizando los dos lemas) y aplicando que el área del triángulo ceviano relativo al circuncentro es menor que el área del triangulo medial, llegamos a la desigualdad
La desigualdad anterior la podemos poner en la forma siguiente
de donde se deduce
que, al menos uno de los factores, digamos 
.
Finalmente, basta observar entonces que
lo que termina la demostración.
---oooOooo---