Problema 576
Consideremos los
triángulos de área 1
¿Cuál es el área máxima
de un cuadrado contenido en uno de ellos?
Halmos,
P. (2000) Problèmes pour mathématiciens, petits el grands. Le sel et le fer
Cassine
(P
201)
Consideraciones
del director.
A)Consideremos
en primer lugar el triángulo equilátero.
Sea
A,B,C. Consideremos A (0,0), 
, 
.
El
cuadrado formado por la altura del vértice C tiene por vértices:
, 
, 
, 
La
recta AU tiene de ecuación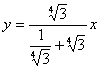 
La
recta BC tiene de ecuación: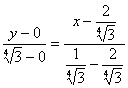 
La
intersección de ambas rectas es el punto de coordenadas:
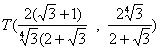
Así el cuadrado inscrito
tiene de lado la ordenada de T, y de área:
; Veamos que es 
es decir, que 
O, lo que es igual, que 
Este valor es 
B) Consideremos ahora
los triángulos isósceles de base variable.
Sean A(0,0), B(m,0),
C(m/2,2/m) los vértices del triángulo.
Consideremos el cuadrado
de lado la altura en C. Sus vértices son:
, 
,
,
La recta CB es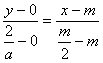 
.
La recta AU es: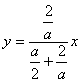
La intersección de ambas
es el punto 
Su ordenada es el lado
del cuadrado pedido.
Así el área es 
.
Derivando e igualando a
0 para obtener el máximo, se tiene:
.
El área pedida corresponde
a la del cuadrado de lado 
que es 0,5
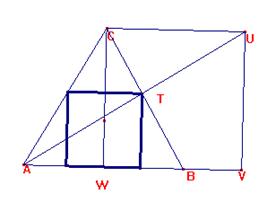
C) Consideremos ahora
los triángulos isósceles con uno de los lados iguales sobre el eje OX.
Sea A(0,0), B(m,0), 
.
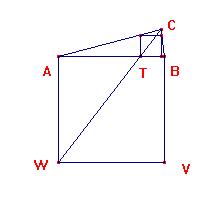
Consideremos el cuadrado
A(0,0), B(m,0), V(m,-m), W(0,-m)
La recta CW tiene por
ecuación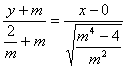 
Dicha recta corta a la
recta AB, eje x en 
La recta AC es 
La perpendicular por T
al eje x corta a la recta AC en 
Así ahora el cuadrado
inscrito tiene de lado 
, que al coincidir con el valor anterior, da lugar a que el
área máxima sea la misma, y el triángulo cuestionado también.
D)Consideremos ahora
todos los triángulos de base la unidad:
Sea 1 la base; la altura será 2.
Consideremos A (0,0),
B(1,0), C(m,2).
Sin pérdida de
generalidad, supongamos en primer lugar que 0<m<=1. Tracemos la altura CH
sobre el lado AB y con ella construyamos el cuadrado CHJK, con J sobre el eje
x.
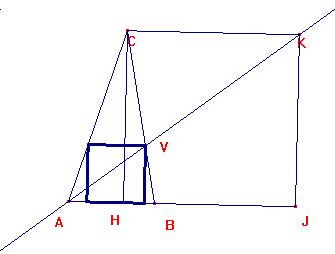
La recta BC tiene de
ecuación
Y la recta AK 
Luego el punto de corte
de ambas es V
,
V es uno de los vértices
del cuadrado inscrito, por lo que todos estos cuadrados inscritos mediante la
correspondiente homotecia del CHJK tienen de lado la ordenada de V y de área 4/9 que
es menor que 0,5.
El no variar esta área
de los cuadrados nos lleva a pensar otra manera de afrontar el problema de
manera que las áreas varíen.
Sea ahora ABC el
triángulo con A (0,0), B(m,0), C(0, 2/m), es decir un triángulo rectángulo con
los catetos sobre los ejes coordenados.
Construyamos el cuadrado
ABHJ, con H(m,m) y J(0,m).
La recta BC tiene de ecuación
.
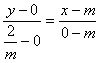La recta AH, es y=x
El punto de corte es 
Es decir, el
correspondiente cuadrado tiene de área 
Derivando e igualando a
0 para obtener el máximo, se tiene:
.
El área pedida es pues
0,5, y el triángulo hallado coincide con el encontrado anteriormente.
E) Sean los triángulos
generales de área 1.
Este apartado se hace
con la ayuda de un colaborador que desea permanecer en el anonimato.
Sea a la base y h la altura
correspondiente. Sea v el lado del cuadrado inscrito
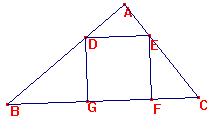
[ABC]=ah/2,
[ADE]= v(h-v)/2, [GDEF]=v2. [BGD]+[EFC]=(a-v)v/2.
Así
es ah/2=v(h-v)/2+v2+(a-v)v/2.
Es
decir, ah=vh+av, Dado que ah=2, debe ser:
2=vh+(2/h)v,
o sea:
, función que ya hemos estudiado y cuyo máximo valor es para
el área del cuadrado ½, con 
, es decir el triángulo rectángulo isósceles de lado 
.
Ricardo
Barroso Campos
Didáctica
de las Matemáticas
Universidad
de Sevilla.