Problema 579.- (Propuesto por Ercole Suppa, profesor titular de matemáticas y física del Liceo Scientifico “A. Einstein”, Teramo, Italia).

Resolución: Vicente Vicario García, I.E.S. El Sur, Huelva.

            A lo largo de la resolución del problema utilizaremos la notación habitual en la geometría del triangulo. Sea entonces  y  debido a la desigualdad triangular. Es bien conocido que por el teorema de los senos generalizado, tenemos

con lo que la longitud del lado c del triangulo ABC coincide con la longitud del radio R de la circunferencia circunscrita al mismo. Por otra parte, a partir de la superficie del triangulo podemos expresar el radio de la circunferencia inscrita r como

            Finalmente, antes de comenzar la resolución del problema emplearemos la conocida relación de Euler para la distancia IO entre el incentro y el circuncentro del triangulo ABC de partida, .

            Comenzaremos suponiendo, sin perdida de generalidad, que  e inicialmente que los puntos D y E pertenecen a las prolongaciones respectivas de los lados BC y AC del triangulo. Por el teorema de los cosenos aplicado al triangulo CDE tenemos que

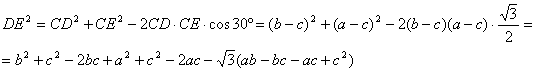
y aplicando el teorema de los cosenos al triangulo ABC de partida, se tiene , con lo que sustituyendo en la expresión anterior, y simplificando

Ya hemos visto que , con lo que puesto que , la proposición queda demostrada si somos capaces de probar la identidad siguiente

Esta última identidad es cierta, puesto que al hacer operaciones algebraicas con sus términos se reducen idénticamente

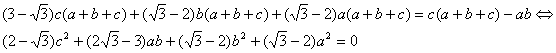
Y esta última identidad se deduce sustituyendo , lo que concluye la demostración de la proposición.

Por otra parte, para determinar otros valores de k que cumplen la relación del problema, se puede comenzar suponiendo que , y , teniendo en cuenta, como ya hemos indicado anteriormente que . Aplicando de nuevo el teorema de los cosenos al triangulo CDE se tiene que

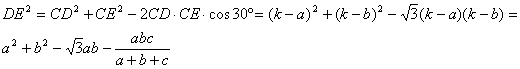
que después de simplificar se reduce a

que podemos poner en la forma

                                  

            Se puede comprobar fácilmente que  es una raíz real de la ecuación cuadrática anterior, con lo que la otra raíz también es real y su valor se puede determinar utilizando la expresión clásica de la suma de las raíces de una ecuación de segundo grado la cual no tiene sentido para nuestro planteamiento geométrico inicial ya que  o bien  toman un valor negativo. De forma análoga se plantea la posibilidad para el caso en el que los puntos D y E estén uno de ellos en la prolongación del lado y el otro sobre el propio lado, teniendo en cuenta ahora que  y con el mismo tratamiento anterior.

---oooOooo---