Problema 580. (Propuesto por J. Bosco Romero, profesor colaborador de la Universidad de Valladolid).

            Sea ABC un triangulo de lados  y D, E, y F los pies de las alturas trazadas desde los vértices A, B y C sobre los lados BC, AC, y AB, respectivamente. Probar que:

(a) . Estudiar todas las desigualdades que se obtienen para cada clase de triangulo según los ángulos

(b) Si c, C son lado y ángulo fijos correspondientes y a y b variables, calcular el valor de

Resolución: Vicente Vicario García, I.E.S. El Sur, Huelva.

(a)        A lo largo de la resolución del problema utilizaremos la notación habitual en la geometría del triangulo. Supondremos inicialmente que el triangulo ABC de partida es acutángulo, con lo que los pies de las alturas pertenecen al interior de cada uno de los  lados del mismo. Para demostrar las desigualdades , es suficiente con sustituir los términos de las mismas para obtener

            La primera desigualdad es cierta. Teniendo en cuenta que , entonces tenemos

            Para demostrar la segunda desigualdad podemos observar que claramente tenemos las relaciones , y utilizando las expresiones trigonometricas relativas al Angulo mitad, tenemos que

           

            Por otra parte, a partir del teorema de los senos, sabemos que

           

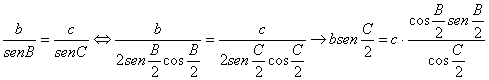
que sustituyendo en la expresión anterior nos da

           

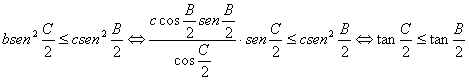
y la ultima desigualdad es claramente cierta, por la hipótesis .

            Por otra parte, si el triangulo dado ABC fuese rectángulo, entonces A seria el ángulo recto y evidentemente los puntos D y F coinciden en el vértice A del triangulo, con lo que la primera desigualdad se transforma en igualdad.

            Si el triangulo dado es isósceles, (o equilátero), entonces podemos tener dos posibilidades: o bien , o bien (o en el caso equilátero). En el primer caso las dos desigualdades se transforman en igualdades pero no en el segundo. Finamente, si el triangulo es obtusángulo, entonces A>90º , las desigualdades siguen siendo ciertas.

(b)       Supondremos ahora que c y C son fijos y a y b variables. Sea . Teniendo en cuenta las expresiones clásicas que se deducen del teorema de los cosenos, entonces

           

ya que, puesto que , entonces  y , con lo que .

            Así pues, utilizando esta expresión y empleando relaciones trigonometricas elementales, podemos determinar

           

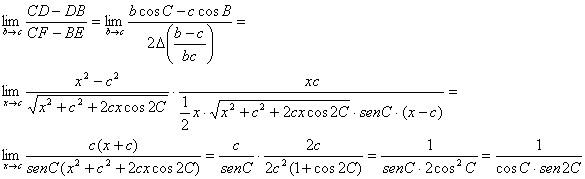
donde el valor del límite propuesto se puede escribir de varias formas equivalentes.

---oooOooo---