Problema 581

Dos circunferencias que no intersecan son tangentes a un ángulo agudo XOY=α.

Construir un triángulo isósceles ABC con el vértice A sobre OX y la base BC sobre OY, tal que cada uno de sus lados iguales sea tangente a cada una de las circunferencias.

 Honsberger, R. (2003): Mathematical Diamonds. The Mathematical Association of America. Washington. D.C. (p. 68)

Solución del director

Supongamos el problema resuelto.

Sea 2β el ángulo ABO.

Es: <OAB=180-α-2β.

Sean O₁ y O₂ los centros de las circunferencias.

Es <AOO₁=α/2, por lo que <AO₁O=180-<OAO₁-AOO₁=180-(90-α/2-β)-α/2= 90+β.

Así, <AO₁O₂=90-β

 

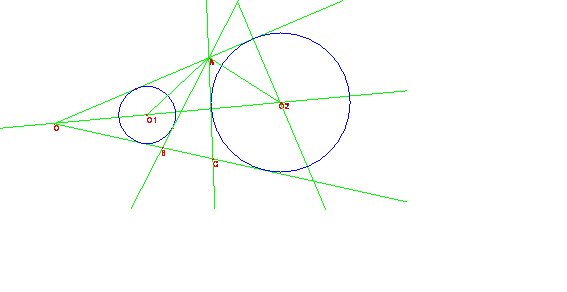
Por otra parte, es <ACB=<ABC=180-<ABO=180-2β.

<BAC=180-<ABC-<ACB=4β-180.

Sea T el punto de tangencia de la circunferencia de centro O₂ con la recta OA

<CAT=180-<BAO-<BAC=180-(180-α-2β)-(4β-180)=180+α-2β.

Así es <O₂AC=90+α/2-β.

Y <O₂AO=180-<O₂AT=90-α/2+β

Por ello, <AO₂O=180-<AOO₂-<O₂AO=180-α/2-(90-α/2+β)=90-β.

De esta manera se concluye que el triángulo AO₁O₂ debe ser _también isósceles.

Por tanto el punto A es la intersección de la mediatriz de O₁O2 con la semirrecta OX