Problema 581.
Dues circumferències que no s’intersecten són tangents a un angle agut 
.
Construïu un triangle isòsceles 
amb el vèrtex A sobre OX i la base 
sobre OY, tal que cadascun dels costats iguals siga tangent a cadascuna de les circumferències.
Honsberger, R. (2003): Mathematical Diamonds. The Mathematical Association of
Solució de Ricard Peiró:
Suposem el problema resolt.
Siga 
el centre de la circumferència menuda que és en centre de la circumferència inscrita al triangle 
.
Aleshores, 
.
Siga 
el centre de la circumferència gran que és en centre de la circumferència exinscrita al triangle 
.
Aleshores,. 
.
Les rectes 
s’ntersecten en el punt D.
El quadrilàter ABDC és inscriptible en una circumferència.
Aleshores El punt A pertany a la mediatriu del segment 
.
Aquesta és la construcció:
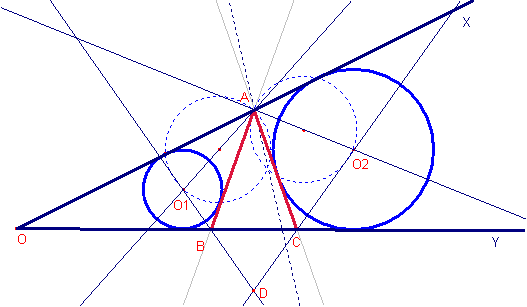
a) Dibuixar la mediatriu del segment .
b) A és la intersecció de la mediatriu anterior i la semirecta OX.
c) Dibuixar la recta r tangent a la circumferència menuda que passa per A.
d) La intersecció de la recta r i la semirecta OY és B
e) Dibuixar la recta s tangent a la circumferència gran que passa per A.
f) La intersecció de la recta s i la semirecta OY és C.
g) Dibuixar el triangle .