Problema 581.
Dos circunferencias que no se intersectan son tangentes a un ángulo agudo 
.
Construir un triángulo isósceles 
con el vértice A sobre OX i la base 
sobre OY, tal que cada uno de los lados iguales sea tangente a cada una de las circunferencias.
Honsberger, R. (2003): Mathematical Diamonds. The Mathematical Association of
Solución de Ricard Peiró:
Supongamos el problema resuelto.
Sea 
el centro de la circunferencia pequeña que es el centro de la circunferencia inscrita al triángulo 
.
Entonces, 
.
Sea 
el centro de la circunferencia grande que es en centro de la circunferencia exinscrita al triángulo 
.
Entonces,. 
.
Las rectas 
se ntersectan en el punto D.
El cuadrilátero ABDC es inscriptible en una circunferencia.
Entonces El punto A pertenece a la mediatriz del segmento 
.
Esta es la construcción:
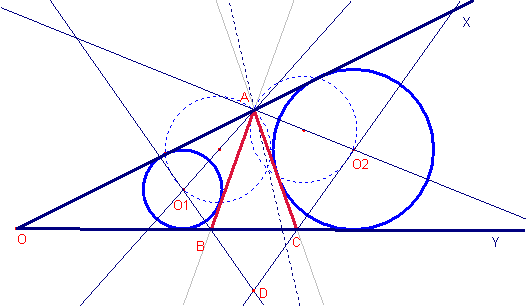
a) Dibujar la mediatriz del segmento .
b) A es la intersección de la mediatriz anterior y la semirecta OX.
c) Dibujar la recta r tangente a la circunferencia pequeña que pasa por A.
d) La intersección de la recta r y la semirecta OY es B
e) Dibujar la recta s tangente a la circunferencia grande que pasa por A.
f) La intersección de la recta s y la semirecta OY es C.
g) Dibujar el triángulo .