Problema 583.- (Propuesto por Ercole Suppa, profesor titular de matemáticas y física del Liceo Scientifico “A. Einstein”, Teramo, Italia).

Sea dado un triangulo ABC, y denotemos respectivamente con O, I, H, G, K el circuncentro, incentro, ortocentro, baricentro y punto de Lemoine. Sea M el punto medio del lado AC, sea N el punto de intersección de la recta AB con la mediatriz de AC y sea g la circunferencia circunscrita al triangulo BNC. Probar que:

(a) El punto O pertenece a la circunferencia g

(b) El punto I pertenece a la circunferencia g si y solo si

(c) El punto H pertenece a la circunferencia g si y solo si , o , o , o

(d) El punto G pertenece a la circunferencia g si y solo si

(e) El punto K pertenece a la circunferencia g si y solo si ( es decir, el triangulo ABC es automediano)

Suppa, E. (2010): Comunicación personal.

Resolución: Vicente Vicario García, I. E. S. “El Sur”, Huelva

A lo largo de la resolución del problema utilizaremos la notación habitual en la geometría del triangulo.

(a) Es claro que el triangulo NAM es rectángulo debido a la construcción, por lo que tenemos que . Por otra parte, es bien conocido por propiedades geométricas elementales de los ángulos en una circunferencia que . Por tanto, para demostrar que O pertenece a la circunferencia g (circunscrita al triangulo BNC) basta con probar que (puesto que el cuadrilátero NBOC es cíclico) , lo que es inmediato ya que . Es claro además que la demostración es valida para ángulos A agudos u obtusos.

(b) Es bien conocido que , por lo que para que I pertenezca a la circunferencia g es necesario y suficiente que , que nos lleva a . Inversamente, si es inmediato comprobar que

(c) Es bien conocido también que , (independientemente del triangulo de partida), y si suponemos que es acutángulo entonces H pertenece a la circunferencia g si se cumple (debido a que el cuadrilátero NBHC es cíclico)

Obviamente, si el triangulo ABC es rectángulo en A entonces la recta MN es paralela a la recta AB y no hay punto de corte.

Si el triangulo es obtusángulo es claro que sigue siendo cierto que y en consecuencia, tras un calculo elemental sencillo, es fácil ver que el ortocentro H pertenece a la circunferencia g si se cumple

Además, si , o bien es obvio que ABC es rectángulo en B o en C, respectivamente, con lo que , o bien , y en consecuencia el ortocentro pertenece a la circunferencia g.

(d) Es claro, por lo ya expuesto que, para que G pertenezca a la circunferencia g es necesario que

Por otra parte, son bien conocidas las expresiones , . Además, utilizando el teorema de los cosenos se obtienen fácilmente las expresiones clásicas (teorema de Apolonio)

,

Por el teorema de los cosenos aplicado al triangulo BGC, tenemos que

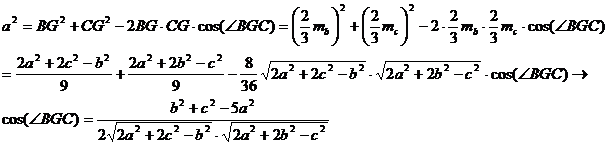
Por otra parte, es sencillo obtener

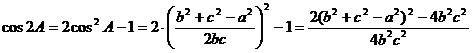
Finalmente, puesto que , y después de simplificar, llegamos a

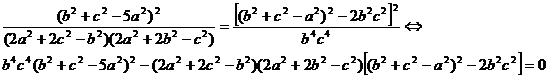
que se puede factorizar en la forma

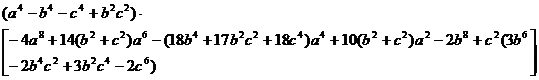
lo que demuestra la proposición.

(e) Según el teorema de von Aubel para cevianas concurrentes particularizado para el caso de las simedianas y denotando por el pie de la simediana que parte del vértice A, se tiene

que junto con la relación obvia , y teniendo en cuenta la expresión clásica entre la mediana y la simediana que parten de un mismo vértice

por lo que es ahora sencillo llegar a la expresión

y de forma similar ara las expresiones de BK y CK.

Para que el punto de Lemoine K pertenezca a la circunferencia g es necesario que . Aplicando el teorema de los cosenos al triangulo BKC tenemos que

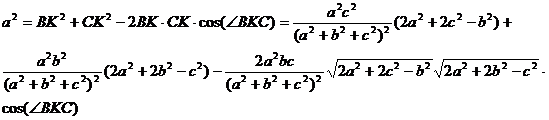
de donde podemos despejar

Finalmente, igualando las expresiones , tenemos que

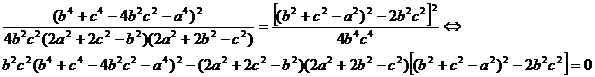
expresión que se puede factorizar en la forma siguiente

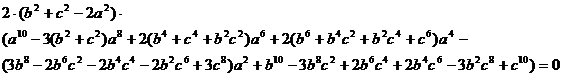
lo que demuestra la proposición.

---oooOooo---