Problema 588.- (Propuesto por Ercole Suppa, profesor titular de matemáticas y física del Liceo Scientifico “A. Einstein”, Teramo, Italia).

            Dado el triangulo acutángulo ABC, sean , , los pies de las alturas trazadas desde los vértices A, B, C, respectivamente. Si denotamos por r, , ,  los inradios de los triángulos ABC, , , , demostrar que:      

Resolución: Vicente Vicario García, I.E.S. El Sur, Huelva.

            A lo largo de la resolución del problema utilizaremos la notación habitual en la geometría del triangulo. Previamente necesitamos un lema que demostramos a continuación.

Lema: “ En todo triangulo ABC se tiene  ”.

Demostración: Con la notación habitual demostraremos que para un triángulo ABC y siendo A un ángulo del mismo, entonces  cosA  es una raíz real de la ecuación poli nómica  siguiente:.

Para la demostración, consideremos las relaciones  (teorema de los senos generalizado) y  (relacionada con el incentro). Entonces, utilizando las identidades trigonométricas del ángulo doble

elevando al cuadrado y operando se tiene

           

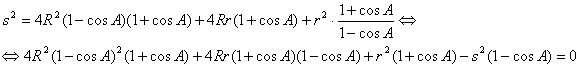
de donde, después de manipulaciones algebraicas, llegamos a la relación que queremos

Claramente esta relación se cumple también para  y . De las relaciones de Cardano-Vieta entre las raíces y los coeficientes deducimos las relaciones

      

donde la primera de estas expresiones es la que aparece en el lema, lo que concluye la demostración del mismo.    ■

            Centrándonos ahora en la resolución del problema, podemos observar que los puntos , , son los vértices del triangulo órtico del triangulo ABC. En consecuencia, y como es bien sabido, los triángulos,, son semejantes al triangulo ABC con razones de homotecia respectivas , , , por lo que, designando [ABC] al área del triangulo de partida y [] el del triangulo , etc., claramente tenemos que

                       

y similarmente para los inradios y . De esta forma, podemos demostrar ya la primera desigualdad, ya que, claramente

                                  

            Para demostrar la segunda, basta con observar que

y el problema concluye puesto que , por la famosa desigualdad de Euler.

                                                           ---oooOooo---