Propuesto por Vicente Vicario García, I.E.S. “El Sur”, Huelva
Problema 589.-
Sea {ABC} un conjunto de triángulos tales que el ángulo A y su lado c en cada uno de ellos son fijos. Denotamos por ![]() ,
, ![]() ,
, ![]() ,
, ![]() la mediana, simediana, ceviana Gergonne y ceviana Nagel que parten del vértice A de cada uno de los mismos, respectivamente. Determinar el valor del siguiente límite cuando la longitud del lado b tienda a la del lado c, es decir, cuando el triangulo ABC tienda a ser isósceles:
la mediana, simediana, ceviana Gergonne y ceviana Nagel que parten del vértice A de cada uno de los mismos, respectivamente. Determinar el valor del siguiente límite cuando la longitud del lado b tienda a la del lado c, es decir, cuando el triangulo ABC tienda a ser isósceles:
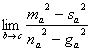
Resolución: Vicente Vicario García, I.E.S. “El Sur”, Huelva.
A lo largo de la resolución del problema utilizaremos la notación habitual en la geometría del triangulo. Inicialmente determinaremos expresiones para ![]() ,
, ![]() ,
, ![]() ,
, ![]() en función exclusiva del ángulo A, el lado c (que son fijos) y el lado variable
en función exclusiva del ángulo A, el lado c (que son fijos) y el lado variable ![]() .
.
Para determinar ![]() basta con aplicar el teorema de los cosenos y llegar a la expresión clásica (teorema de Apolonio)
basta con aplicar el teorema de los cosenos y llegar a la expresión clásica (teorema de Apolonio)
![]()
Para determinar ![]() basta con utilizar la conocida expresión
basta con utilizar la conocida expresión ![]() , obteniendo
, obteniendo
![]()
Para determinar ![]() basta con emplear el teorema de los cosenos, de manera que
basta con emplear el teorema de los cosenos, de manera que
![]()
que después de sustituir, simplificar y utilizar relaciones trigonometricas elementales nos lleva a la expresión siguiente para la ceviana Gegonne
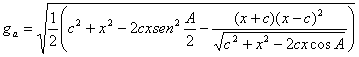
De forma análoga se obtiene, a partir del teorema de los cosenos, una expresión para la ceviana Nagel
![]()
que, de nuevo, después de simplificar y utilizar expresiones trigonometricas elementales nos lleva a
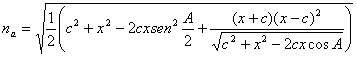
Pasemos ahora a calcular el límite:

que es el valor del mismo.
---oooOooo---