Problema 590.- (Propuesto por J. B. Romero Márquez, profesor colaborador de la Universidad de Valladolid).

            Sea ABC triángulo rectángulo en A, de cateto c fijo y cateto b e hipotenusa a variables. Desde A trazamos la altura , y su bisectriz interior , donde y son los pies sobre BC de la altura y bisectriz interior que parten del vértice A, respectivamente. Calcular el siguiente límite:

Resolución: Vicente Vicario García, I.E.S. El Sur, Huelva.

            A lo largo de la resolución del problema utilizaremos la notación habitual en la geometría del triangulo. Sea . Es sencillo obtener la expresiones para la altura y la bisectriz interior que parten del vértice del ángulo recto A. Para la altura, tenemos que

y, para la bisectriz interior, teniendo en cuenta que A es recto, tenemos que

            Por otra parte, es sencillo determinar , y aplicando el teorema de la bisectriz interior y relaciones geométricas elementales obtenemos

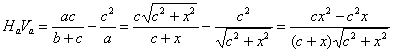
de modo que el límite pedido vale

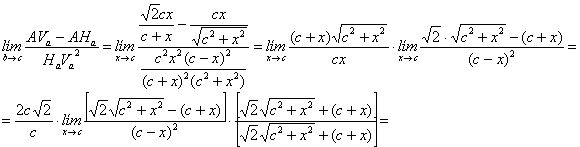
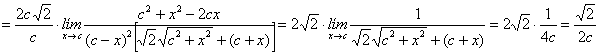
                                                           ---oooOooo---