Problema 591.- (Propuesto por Julián Santamaría Tobar, profesor de Dibujo del I.E.S. La Serna de Fuenlabrada, Madrid).

Resolución: Vicente Vicario García, I.E.S. El Sur, Huelva.

            A lo largo de la resolución del problema utilizaremos la notación habitual en la geometría del triángulo. Tal y como está planteado el problema asumimos que éste quedará resuelto siempre que se identifique el triángulo pedido y no necesariamente una construcción del mismo con regla y compás. Nosotros identificaremos tal triángulo de forma analítica. Pueden darse dos situaciones:

(a) Supongamos que el lado c es el lado desigual (en caso de triángulo equilátero el resultado es trivial). En este caso es claro que el punto T es el punto medio de este lado y que existen infinitos triángulos isósceles que se pueden dar con las condiciones del problema.

(b) Sea ahora c uno de los lados iguales del triángulo isósceles. Es bien sabido que el punto de tangencia T del círculo inscrito con dicho lado, divide el mismo en dos segmentos de longitudes  y . Por otra parte, es claro que

,

            Además, de la relación , tomando tangentes tenemos que

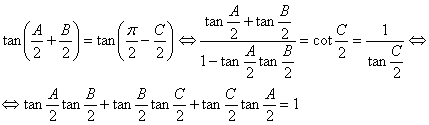
                                                                                                                                 [1]

y como el triángulo es isósceles entonces , y sustituyendo en la expresión [1] anterior

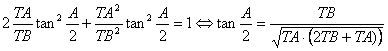
            Finalmente, tenemos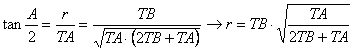

y, en consecuencia, el radio r de la circunferencia inscrita queda determinado en función de valores conocidos, por lo que el triángulo pedido queda completamente identificado. Además, es claro según la expresión obtenida para r que dicho radio es construible con regla y compás ya que sólo involucra sumas, cocientes y raíces cuadradas de términos construibles. Faltaría solamente trazar una perpendicular en T al lado c de longitud r y trazar la circunferencia inscrita (tangente al lado c), lo que concluye el problema.

---oooOooo---