Problema 592
5.5.1 Se tiene un triángulo ABC, donde AB=BC. Si H y S son los puntos medios de AC y HB, respectivamente, y HL es perpendicular a SC en L, pruebe que es <BLA=90
Donaire, M. F. (2010): Formas y números. La geometría en las Olimpíadas Matemáticas. Fondo Editorial del Pedagógico San Marcos. Lima. (p. 180)
Solución del director.
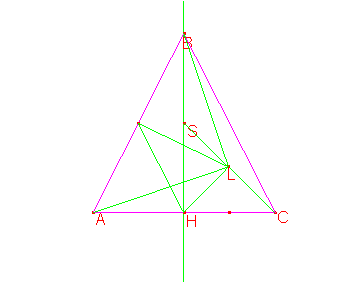
Sea H origen de coordenadas. Sea A(-2,0), C(2,0), y B(0,4m). Es S(0,2m).
La recta SC es (y-2m)/(0-2m)=(x-0)/(2-0), es decir: y=-mx+2m.
La recta HL por tanto tiene de pendiente 1/m y su ecuación es y=(1/m)x.
Así el punto M es tal que (1/m)x=-mx+2m, de donde se tiene:
(m+1/m)x=2m , y así es x=(2m)/(m+1/m)=(2m2)/(1+m2)
Luego L((2m2)/(1+m2), (2m)/(1+m2))
Ahora el vector AL tiene por componentes ((2+4m2)/(1+m2), (2m)/(1+m2) ).
El vector LB tiene por componentes ((-2m2)/(1+m2), (4m3+2m)/(1+m2)).
El producto escalar de ambos es 0, por lo que son perpendiculares, cqd.

2ª solución:
La recta que contiene el punto medio M de AB y el punto medio U de HC es paralelo a SC y por ello es perpendicular a HL. Dado que U es el centro de la circunferencia HLC, la recta MU es mediatriz de LH, así, el triángulo MLH es isósceles por lo que L es un punto de la circunferencia de diámetro BA, cqd.
