Problema 592.- Se tiene un triángulo ABC, donde ![]() . Si H y S son los puntos medios de AC y HB, respectivamente, y HL es perpendicular a SC en L, pruebe que
. Si H y S son los puntos medios de AC y HB, respectivamente, y HL es perpendicular a SC en L, pruebe que ![]() .
.
Donaire, M. F. (2010): Formas y números. La geometría en las Olimpíadas Matemáticas. Fondo Editorial del Pedagógico San Marcos. Lima. (p. 180)
Resolución: Vicente Vicario García, I.E.S. El Sur, Huelva.
A lo largo de la resolución del problema utilizaremos la geometría de coordenadas en el plano. Sin pérdida de generalidad, podemos suponer que el triángulo dado tiene como vértices ![]() ,
, ![]() ,
, ![]() , con b y q reales y positivos. Además, es claro que
, con b y q reales y positivos. Además, es claro que ![]() y
y ![]() . Por otra parte, podemos determinar la ecuación de la recta SC hallando previamente un vector director de la misma, de modo que
. Por otra parte, podemos determinar la ecuación de la recta SC hallando previamente un vector director de la misma, de modo que
![]()
con lo que la ecuación de la recta SC vendrá dada por
![]()
Es bien sabido que dos rectas son perpendiculares si y sólo si el producto de sus pendientes es ![]() , con lo que podemos determinar la ecuación de la recta HL
, con lo que podemos determinar la ecuación de la recta HL
![]()
Podemos entonces determinar las coordenadas del punto L como solución del sistema de ecuaciones siguiente
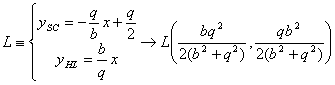
Finalmente, para demostrar que el ángulo BLA es recto, basta con demostrar que el producto escalar de los vectores AL y BL es nulo. Esto es cierto ya que tras un pequeño cálculo se llega a las expresiones
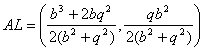 ,
, 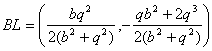
con lo que
![]()
lo que concluye el problema.
---oooOooo---