Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid
Problema 594
Sea ABCD un cuadrado de lado a, y ADE un triángulo rectángulo donde E es el punto medio de DC.
Probar que existen dos puntos F, F´ sobre AE, tales que CF= BF´ y que ambos segmentos son perpendiculares.
Romero, J. B. (2010): Comunicación personal.
Solución del director.
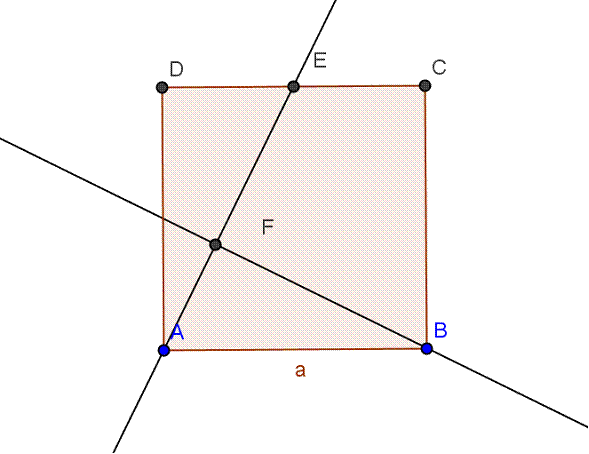
Consideremos la perpendicular desde B a AE.
Cortará a AE en F.
Sea <DEA=α. Es <FAB=90-α, y <FBA=α.
Por la simetría del cuadrado, es <EBC=α, y al ser ECBF un cuadrilátero inscrito, por ser <BFE=<BCE=90, es <EFC=<EBC=α. Por otra parte, <FEC=180-<FED=180-(90-α)=90+α.
Luego <FCE=180-<FEC-<EFC=180-(90+α)-α=90-2α. Por ello, <FCB=2α.
Además, al ser <ABF=α, es <FBC=90-α, y por último
<CFB=180-<FCB-<FBC=180-2α-(90-α)=90-α.
Así pues el triángulo FCB es isósceles y CF=CB=a

Sea F’ tal que DF’ la construimos perpendicular a AE. Al ser la figura análoga, por consideraciones similares es BF’=BC=a, y <CBF’=90-2α.
Luego BF’ y CF son también perpendiculares .
Ricardo Barroso Campos.
Didáctica de las Matemáticas
Universidad de Sevilla