Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid
Problema 594
Sea ABCD un cuadrado de lado a, y ADE un triángulo rectángulo donde E es el punto medio de DC.
Probar que existen dos puntos F, F´ sobre AE, tales que CF= BF´ y que ambos segmentos son perpendiculares.
Romero, J. B. (2010): Comunicación personal.
Solución de Juan Bosco Romero Márquez, profesor colaborador de
: Método de coordenadas cartesianas.
Supongamos que el problema está resuelto.
Tomamos, D(0,0) , C(a,0), B(a,a) y A(0,a) y E(a/2, 0).
F es la intersección de las rectas AE y BF que son perpendiculares. Escribiendo las ecuaciones de dichas rectas y resolviendo el sistema lineal de ecuaciones que se obtiene siguiente :
![]()
Similarmente, F´ se obtiene como el pie de la perpendicular de la altura, trazada desde D a AE.
![]()
Probemos primero que BF´= CF.
En efecto :
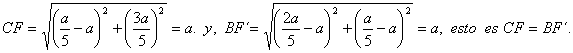
Veamos que, CF y BF´ son perpendiculares tomados como vectores.
En efecto :
Los vectores :
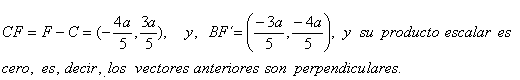
Avila, 29 de Octubre, 2010.
Juan-Bosco Romero Márquez