Propuesto por Juan Bosco Romero Márquez,
profesor colaborador de
Problema 594
Sea ABCD un cuadrado de lado a, y ADE un triángulo rectángulo donde E es el punto medio de DC.
Probar que existen dos puntos F, F´ sobre AE, tales que CF= BF´ y que ambos segmentos son perpendiculares.
Romero, J. B. (2010): Comunicación personal.
Resuelto por JULIÁN SANTAMARÍA TOBAR
profesor de Dibujo del IES
 Se
va a comenzar estudiando el problema resuelto. En el cuadrilátero BCF´F se
conocen cinco datos: el ángulo de las diagonales BF’ y CF, igualdad de las
diagonales, lado BC, ángulo de los lados BC y FF’, la distancia del vértice B
al lado FF’(o a la recta AF).
Se
va a comenzar estudiando el problema resuelto. En el cuadrilátero BCF´F se
conocen cinco datos: el ángulo de las diagonales BF’ y CF, igualdad de las
diagonales, lado BC, ángulo de los lados BC y FF’, la distancia del vértice B
al lado FF’(o a la recta AF).
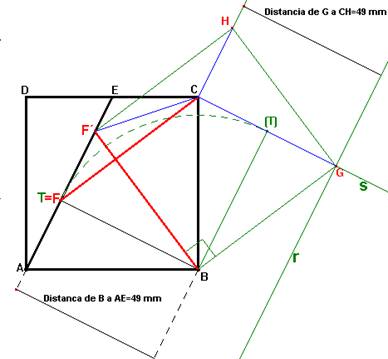
Para agrupar las propiedades de otro modo se va a realizar una transformación del cuadrilátero en un paralelogramo. Se trasladan los lados FF’ y FB mediante la dirección y magnitud de la diagonal FC resultando los segmentos CH y CG. De este modo el paralelogramo BGHF’ tiene por lados y ángulos los que corresponden a las diagonales del cuadrilátero BCF´F (en este caso particular paralelogramo es un cuadrado) además los lados y ángulos del cuadrilátero son las líneas y ángulos que parten del punto C y unen los vértices BGHF’ del cuadrado.
El punto G esta sometido a dos condiciones. Por una parte, la distancia del punto G al segmento CH es la misma que la distancia del vértice B a la recta AE por lo tanto el vértice G está en una recta r paralela a CH cuya distancia es conocida. Por otra parte al girar el punto F’ 90º respecto al centro de giro B da como resultado el vértice G; el punto F’ se desconoce pero al girar la recta AE se giran todos sus puntos; para girar la recta AE se gira 90º el radio BT perpendicular a la recta AE y da como resultado el radio B(T) y la recta AE se transforma con el giro en la recta s. En definitiva, el punto G corresponde a la intersección de las recta r y s, con este punto se construye el cuadrado BGHF’ y al deshacer la traslación se obtienen los F y F’ pedidos.