Problema 594

Sea ABCD un cuadrado de lado a, y ADE un triángulo rectángulo donde E es el punto medio de DC.

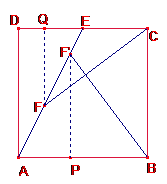Probar que existen dos puntos F, F´ sobre AE, tales que CF= BF´ y que ambos segmentos son perpendiculares.

Romero, J. B. (2010): Comunicación personal.

Solución de Ricard Peiró:

Supongamos el problema resuelto.

Sea P la proyección de F’ sobre el lado .

Sea Q la proyección de F sobre el lado .

Como , .

Como , los triángulos rectángulos ,  son iguales, entonces:

,  .

Los triángulos ,  son semejantes, aplicando el teorema de Tales:

Los triángulos ,  son semejantes, aplicando el teorema de Tales:

Determinemos :

Entonces:

.

Resolviendo la ecuación, .

Por tanto el problema tiene solución única.