Problema 594.- (Propuesto por J. B. Romero Márquez, profesor colaborador de
Sea ABCD un cuadrado de lado a, y ADE un triángulo rectángulo donde E es el punto medio de DC. Probar que existen dos puntos F y F´ sobre AE tales que 
y que ambos segmentos son perpendiculares.
Resolución: Vicente Vicario García, I.E.S. El Sur, Huelva.
Demostraremos que existen los puntos F y F´ que anuncia el problema. Para ello, basta con considerar 
y F sobre AE con . Es claro, aplicando el teorema de Pitágoras que
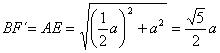
Por otra parte, denotamos 
. Es bien conocida (y fácil de deducir) la expresión que determina el área de un cuadrilátero convexo como la mitad del producto de sus diagonales por el seno del ángulo que formas las mismas. De esta forma, determinaremos el área del cuadrilátero FBCF´ en función de x e imponiendo la condición de perpendicularidad sobre sus diagonales, calcularemos su valor. Entonces, denotando por [XYZ] el área del triángulo XYZ y por [XYZW] el área del cuadrilátero XYZW, es sencillo ver que
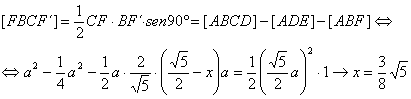
que obviamente es compatible con las condiciones del problema, lo que concluye la resolución del mismo.
---oooOooo---