Problema 595.
La altura ![]() de un triángulo
de un triángulo ![]() interseca a la circunferencia circunscrita a
interseca a la circunferencia circunscrita a ![]() en P. La recta de Simson de P respecto a
en P. La recta de Simson de P respecto a ![]() es paralela a la recta tangente por A a la circunferencia circunscrita.
es paralela a la recta tangente por A a la circunferencia circunscrita.
D'Ignazio, I. y Suppa, E. (2001): Il problema geometrico dal compasso al cabri Interlinea Editrice. Téramo. (p. 276)
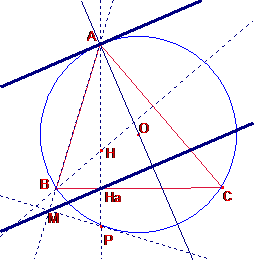 Solució Ricard Peiró:
Solució Ricard Peiró:
Considerem el triangle en les següents coordenades cartesianes:
![]() .
.
Les coordenades de ![]() són
són ![]() .
.
Siga ![]() ortocentre del triangle. Calculem y:
ortocentre del triangle. Calculem y:
![]()
 .
.
Resolent l’equació: ![]() . Aleshores,
. Aleshores, ![]() .
.
![]() .
.
Calculem les coordenades de l’ortocentre:
La recta que passa per B i és perpendicular al costat ![]() té equació:
té equació:
![]() .
.
La recta que passa per A i és perpendicular al costat ![]() té equació:
té equació:
![]() .
.
La intersecció de les rectes ![]() és l’ortocentre H que té coordenades:
és l’ortocentre H que té coordenades:
![]() .
.
La recta ![]() talla la circumferència circumscrita en el punt P.
talla la circumferència circumscrita en el punt P.
![]() , aleshores, P és el simètric de H respecte de
, aleshores, P és el simètric de H respecte de ![]() . Les coordenades de P són:
. Les coordenades de P són:
![]() .
.
Siga M la projecció de P sobre el costat ![]() . Determinem les seues coordenades.
. Determinem les seues coordenades.
La recta que passa pels punts A, B té equació:
![]() .
.
La recta que passa per P i és perpendicular a la recta ![]() té equació:
té equació:
![]() .
.
La intersecció de les rectes ![]() és M que té coordenades:
és M que té coordenades:
![]()
La recta de Simson de P respecte del triangle ![]() , és la recta que passa pels punts M,
, és la recta que passa pels punts M, ![]() . El seu vector director és:
. El seu vector director és:
![]() .
.
Vegem que els vectors ![]() ,
, ![]() són ortogonals:
són ortogonals:
![]()
Aleshores, la recta de Simson de R respecte del triangle ![]() és paral·lela a la tangent per A a la circumferència circumscrita.
és paral·lela a la tangent per A a la circumferència circumscrita.