Problema 595.
La altura ![]() de un triángulo
de un triángulo ![]() intersecta la circunferencia circunscrita a
intersecta la circunferencia circunscrita a ![]() en P.
en P.
La recta de Simson de P respecto del triángulo ![]() és paralela a la tangente por A a la circunferencia circumscrita.
és paralela a la tangente por A a la circunferencia circumscrita.
D'Ignazio, I. y Suppa, E. (2001): Il problema geometrico dal compasso al cabri Interlinea Editrice. Tieneramo. (p. 276)
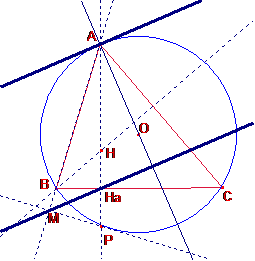 Solució Ricard Peiró:
Solució Ricard Peiró:
Consideremos el triángulo con las seguientes coordenadas cartesianas:
![]() .
.
Las coordenadas de ![]() son
son ![]() .
.
Sea ![]() ortocentro del triángulo. Calculemos y:
ortocentro del triángulo. Calculemos y:
![]()
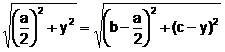 .
.
Resolviendo la ecuación: ![]() . Entonces,
. Entonces, ![]() .
.
![]() .
.
Calculemos las coordenadas del ortocentro:
La recta que pasa per B i és perpendicular al lado ![]() tiene ecuación:
tiene ecuación:
![]() .
.
La recta que pasa por A y es perpendicular al lado ![]() tiene ecuación:
tiene ecuación:
![]() .
.
La intersecció de las rectas ![]() es el ortocentro H que tiene coordenadas:
es el ortocentro H que tiene coordenadas:
![]() .
.
La recta ![]() corta la circunferencia circumscrita en el punto P.
corta la circunferencia circumscrita en el punto P.
![]() , entonces, P es el simétrico de H respecto de
, entonces, P es el simétrico de H respecto de ![]() . Las coordenadas de P son:
. Las coordenadas de P son:
![]() .
.
Sea M la projecció de P sobre el lado ![]() . Determinemos sus coordenadas.
. Determinemos sus coordenadas.
La recta que pasa por los puntos A, B tiene ecuación:
![]() .
.
La recta que pasa per P y és perpendicular a la recta ![]() tiene ecuación:
tiene ecuación:
![]() .
.
La intersección de las rectas ![]() és M que tiene coordenadas:
és M que tiene coordenadas:
![]()
La recta de Simson de P respecto del triángulo ![]() , es la recta que pasa por los puntos M,
, es la recta que pasa por los puntos M, ![]() . Su vector director es:
. Su vector director es:
![]() .
.
Veamos que los vectores ![]() ,
, ![]() son ortogonales:
son ortogonales:
![]()
Entonces, la recta de Simson de R respecte del triángulo ![]() es paralela a la tangente por A a la circunferencia circunscrita.
es paralela a la tangente por A a la circunferencia circunscrita.