Problema 596.
Siga P un punt interior al triangle ![]() i siguen les cevianes
i siguen les cevianes ![]()
![]() .
.
Es fan les construccions de tots els rombes indicats en la figura.
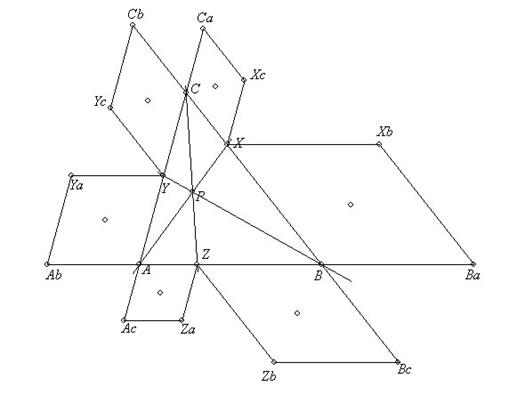
Denotem per ![]() l’àrea de cadascun dels rombes
l’àrea de cadascun dels rombes
AZZaAc, AYaAb, CYYcCb, XCCaXc, XBBaXb, ZBBcZb, respectivament.
Proveu que es verifica la relació entre les àrees següents:
![]() si i només si
si i només si ![]() concorren en el punt P..
concorren en el punt P..
Solució de Ricard Peiró:
Utilitzarem el teorema de Ceva que diu:
Teorema de Ceva:
Siga el triangle ![]() , siguen els punts
, siguen els punts ![]() .
.
Aleshores, els segments ![]() es tallen en un punt P Û
es tallen en un punt P Û ![]() .
.
Calculem les àrees ![]() :
:
![]() ,
, ![]() .
.
![]() ,
, ![]() .
.
![]() ,
, ![]()
Aleshores,:
![]()
![]()
![]()
![]()
![]()
Simplificant:
![]()
![]()
![]()
![]()
![]()
![]()
Û ![]()
Aplicant el teorema de Ceva:
![]()
![]()
![]() concorren en el punt P.
concorren en el punt P.