Problema 596.

Sea un P punto interior al triángulo , con su triángulo correspondiente ceviano XYZ.

Se hacen las construcciones de todos los rombos indicados en la figura.

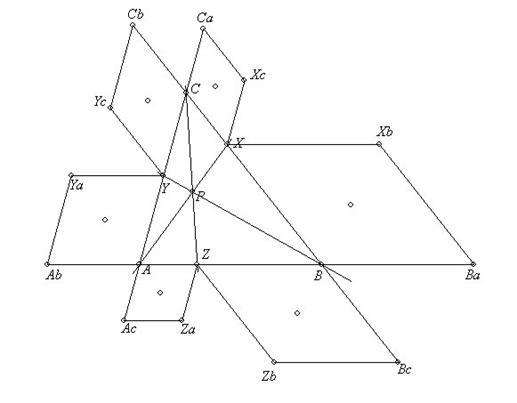
Denotamos por , el área de cada uno de los rombos AZZ_aA_c, AY_aA_b, CYY_cC_b, XCC_aX_c, XBB_aX_b, ZBB_cZ_b, respectivamente.

Probar que se verifica la relación entre las áreas siguientes:

    si y sólo si , concurren en el punto P.

Solución de Ricard Peiró:

Utilizaremos el teorema de Ceva que dice:

Teorema de Ceva:

Sea el triángulo , sea los puntos .

Entonces, los segmentos  se cortan en un punto P  Û  

Calculemos las áreas :

,    .

,                                   .

,                                    

Entonces,:

       

             

Simplificando:

               

             

Û      

Aplicando el teorema de Ceva:

        concurren en el punto P.