Problema 597.

Són necessàriament iguals dos triangles acutangles i isòsceles, que tinguen el mateix radi del cercle inscrit i també iguals els dos parells de costats laterals?

Solució Ricard Peiró.

Considerem els triangles isòsceles acutangle, .

Siga r el radi de la circumferència inscrita al triangle.

Estudiem els valors possibles de b

Si dividim el triangle  per l’altura queda el triangle rectangle .

Siga , per hipòtesi .

Siga .

Siga T el punt de tangència de la circumferència inscrita i el costat .

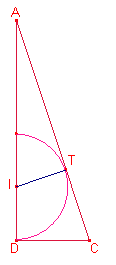Aplicant raons trigonomètriques al triangle rectangle :

.

Aplicant raons trigonomètriques al triangle rectangle :

.

Considerem la funció

,  .

Estudiem la seua monotonia amb la primera derivada:

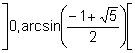 és decreixent en .

 és creixent en .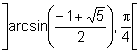

Aleshores, existeixen valors de b que tenen dues antiimatges una en 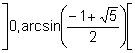 i l’altra en .

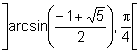El problema té dues solucions quan:

.
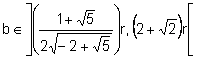