Problema 597

Problema 597.

¿Serán necesariamente iguales dos triángulos acutángulos e isósceles, que tengan el mismo radio del círculo inscrito y también iguales los dos pares de lados "laterales"?

Kvant (1979) M556 (Traducción del ruso de Francisco Bellot Rosado, a quien el director agradece la atención)

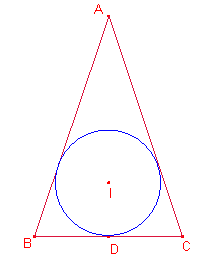
Solución Ricard Peiró.

Consideremos los triángulos isósceles acutángulos, .

Sea r el radio de la circunferencia inscrita al triángulo.

Estudiemos los valores posibles de b

Si dividimos el triángulo por la altura queda el triángulo rectángulo .

Sea , por hipótesis .

Sea

Sea T el punto de tangencia de la circunferencia inscrita y el lado .

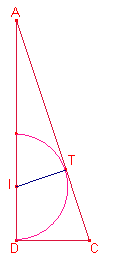Aplicando razones trigonométricas al triángulo rectángulo :

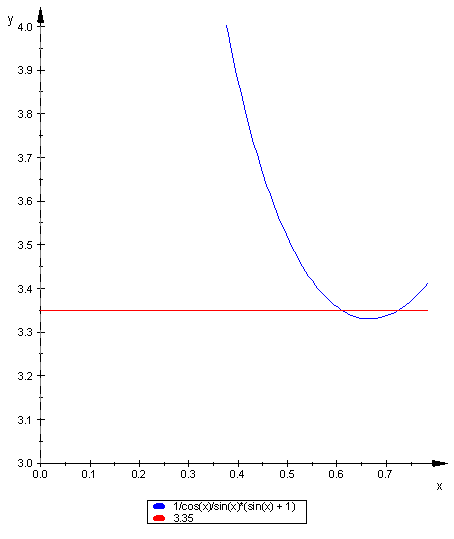
Consideremos la función

, .

Estudiemos la monotonía con la primera derivada:

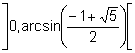es decreciente en .

es creciente en .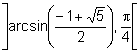

Entonces, existen valores de b que tienen dos antiimágenes una en 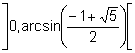i y otra en .

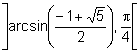El problema tiene dos soluciones cuando:
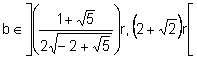