Problema 598.-
Sea ABC un triángulo, tal que AB<AC, y con <BAC=2<BCA. Sobre AC se toma D tal que CD=AB. Por B se traza la recta l paralela a AC. La bisectriz exterior de A interseca a l en M y la paralela por C a AB interseca a l en N. Prueba que MD=DN.
15 Olimpiada Mexicana de Matemática (26-27 Noviembre 2001)
Solución del director
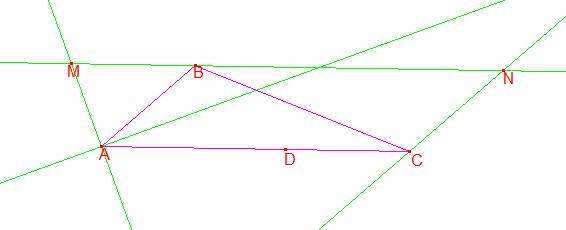
Sea <BCA=α, <BAC=2α
CD=AB por construcción.
CN paralela a AB, luego es CN=AB.
CN=CD=AB. Así, CND es un triángulo isósceles.
<DCN=180-2α, de donde <CDN=<CND=α.
<MAB=90-α, por ser bisectriz externa.
<MBA=2α por construcción.
Luego <AMB=90-α
De ello se deduce que MA=MB.
Así MBCD es un paralelogramo, y <DMB=α=<DNM.
Es decir el triángulo DMN es isósceles, y DM=DN, cqd.
Ricardo Barroso Campos
Didáctica de las Matemáticas.
Universidad de Sevilla.