Problema 611
Desafíos.
1.- Hallar el ángulo ACB (su valor numérico) sabiendo que (ABC) isósceles con AC = BC y que los segmentos AB, AD, DE, EF, FC son iguales. con D,y F sobre BC, con el orden CFDB, y E sobre CA, con E interior.
Dalcín. M (2009): Un estudio sobre la iniciación al pensamiento deductivo en la formación de profesores de matemática. El caso de la geometría. Seminario de Investigación en Matemática Educativa III Programa de Doctorado, CICATA – IPN, México Montevideo, tutorizado por : Dr. Javier Lezama. (p. 153)
Con la autorización de su autor, a quien el director agradece la gentileza.
Solución del director.
Supongamos sin pérdida de generalidad que AC=BC=1, y que <ACB=2γ.
Es AB=2 sen γ.
Así BD/AB=AB/AC, luego BD=4 sen 2γ.
DF es lado del triángulo isósceles EDF, con ED=EF=AB=2 sen γ, y <DFE=4γ.
Por ello es DF=2 (2 sen γ) cos 4 γ.
CF=AB=2 sen γ
Por todo ello, es:
BC=BD+DF+FC= 4 sen 2γ + 2 (2 sen γ) cos 4 γ + 2 sen γ =AC = 1 [*]
Siendo cos 4γ= 1 +8 cos 4 γ-8 cos 2 γ .
Se tiene que la ecuación [*] queda de la siguiente manera:
32 sen 5 γ - 32 sen 3 γ + 4 sen 2 γ +6 sen γ -1=0.
Tal ecuación de grado quinto tiene cinco soluciones:
-0.93969, -0.5, 0.17365, 0.5, 0.76604.
a) El primer valor da lugar a γ=-70º.
Así, adaptando el valor el triángulo es 140, 20, 20.
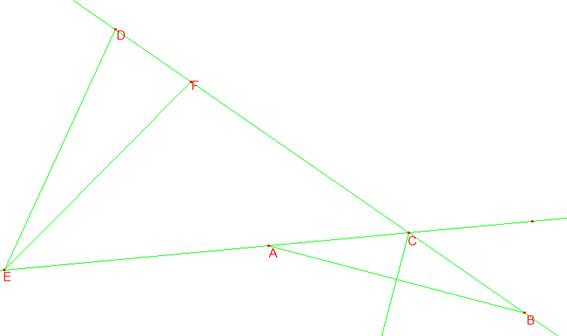
Lógicamente los puntos E, F y D son exteriores a AC y CB, respectivamente, por lo que no se cumple el enunciado del problema.
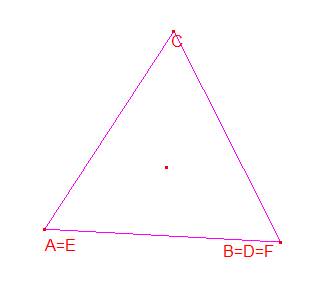
b) El segundo valor es sin γ=-30º, lo que da lugar a un triángulo equilátero, que es una solución degenerada, pues por ejemplo, E=A, y F=D=B.
c) El tercer valor es sin γ=0. 17465.. lo que da como solución el triángulo de ángulos 20º,80º,80º. Lógicamente este resultado es pertinente.
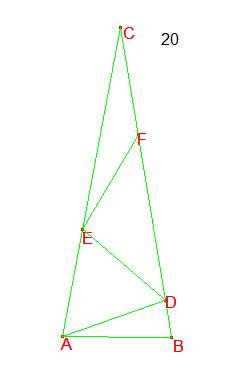
d) El cuarto valor es sin γ=0.5
Es pues el triángulo equilátero. Así, E=A, y F =D= B es una posible interpretación. Sería posiblemente una solución degenerada, al no cumplir estrictamente el enunciado.
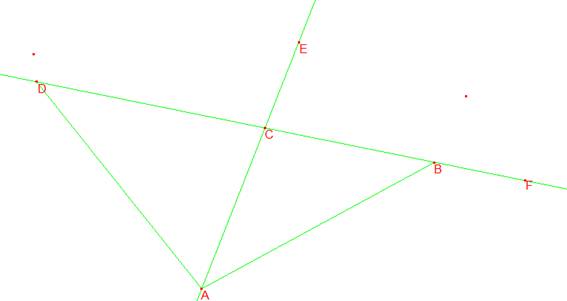
e) El quinto valor da lugar a sen γ=0.76604. De donde γ=50º.
Da lugar al triángulo 100º 40º 40º, lo que de nuevo incumple las condiciones del enunciado.
Ricardo Barroso Campos
Didáctica de las Matemáticas
Universidad de Sevilla