Problema 617.
Resoleu el triangle ![]() coneguts b, a+c,
coneguts b, a+c, ![]() .
.
Solució de Ricard Peiró:
![]() .
.
El problema té dues solucions si ![]() i
i ![]() .
.
El problema té una solució si ![]() i
i ![]() .
.
El problema no té solució si ![]() o
o ![]() .
.
Dos mètodes de construcció:
Mètode 1:
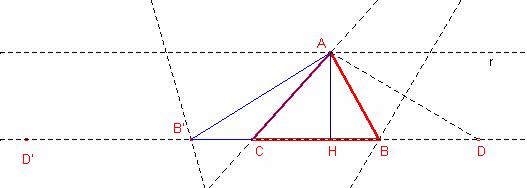
Dibuixar ![]() .
.
Dibuixar una recta r paral·lela a CD a una distància ![]() .
.
Dibuixat la circumferència de radi b i centre C que talla la recta r en A.
Dibuixar la mediatriu al segment ![]() que talla la recta CB en el punt B.
que talla la recta CB en el punt B.
Dibuixar el triangle ![]()
Dibuixar ![]() .
.
Dibuixar la mediatriu al segment ![]() que talla la recta CB en el punt B’.
que talla la recta CB en el punt B’.
Dibuixar el triangle ![]() .
.
Mètode 2:
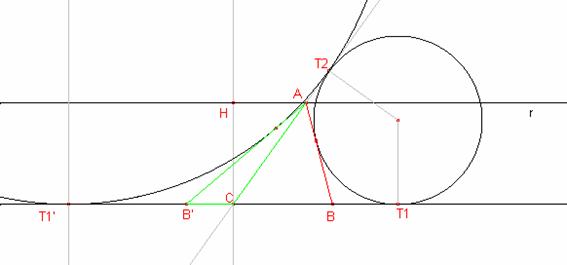
Dibuixar ![]() .
.
Dibuixar una recta r paral·lela a CD a una distància ![]() .
.
Dibuixat la circumferència de radi b i centre C que talla la recta r en A.
Dibuixar la recta CA.
La circumferència de centre C i radi a+b+c talla la recta CA en el punt ![]() .
.
Dibuixem la recta perpendicular a ![]() que passa per
que passa per ![]()
Dibuixem la recta perpendicular a ![]() que passa per
que passa per ![]()
Les dues rectes s’interesecten en l’exincentre del triangle ![]() .
.
Dibuixem la circumferència exincrita.
Dibuixem la recta tangent a la circumferència exincrita que passa per A que talla la recta ![]() en el punt B.
en el punt B.
Dibuixar el triangle ![]()
Dibuixar ![]() .
.
Dibuixem la recta perpendicular a ![]() que passa per
que passa per ![]()
Dibuixem la circumferència exincrita.
Dibuixem la recta tangent a la circumferència exincrita que passa per A que talla la recta ![]() en el punt B’.
en el punt B’.
Dibuixar el triangle ![]() .
.
Exemple particular resolt analíticament:
Resoleu el triangle ![]() coneguts
coneguts ![]() ,
, ![]() ,
, ![]() .
.
Solució:
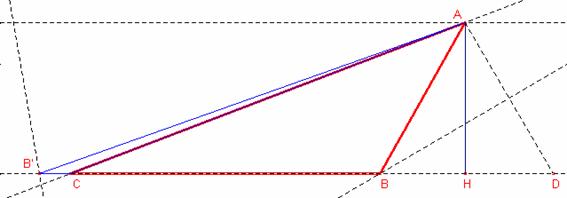 Siga
Siga ![]() altura del triangle.
altura del triangle.
Aplicant raons trigonomètriques al triangle rectangle ![]() :
:
![]() , aleshores:
, aleshores: ![]() .
.
Suposem que ![]() .
. ![]() .
.
Aplicant el teorema del cosinus al triangle ![]() :
: ![]() .
.
Considerem el sistema ![]() la solució del qual és:
la solució del qual és:
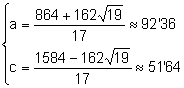 . Tenint en compte que
. Tenint en compte que ![]() B és un angle obtús.
B és un angle obtús.
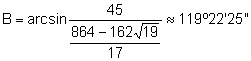 (angle obtús).
(angle obtús). ![]() .
.
Suposem que ![]() .
. ![]() . Fent el mateix procediment:
. Fent el mateix procediment:
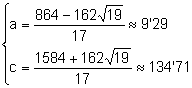 . Tenint en compte que
. Tenint en compte que ![]() l’angle B és agut.
l’angle B és agut.
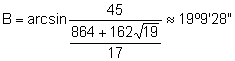 (angle agut).
(angle agut).
![]() .
.