Problema 617.
Resolver el triángulo ![]() conocidos b, a+c,
conocidos b, a+c, ![]() .
.
Solución de Ricard Peiró:
![]() .
.
El problema tiene dos soluciones si ![]() i
i ![]() .
.
El problema tiene una solución si ![]() i
i ![]() .
.
El problema no tiene solución si ![]() o
o ![]() .
.
Dos métodos de construcción:
Método 1:
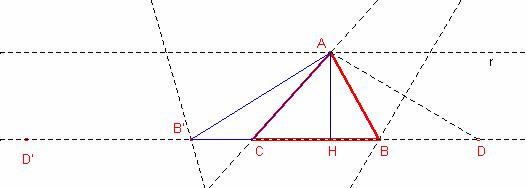
Dibujar ![]() .
.
Dibujar una recta r paralela a CD a una distancia ![]() .
.
Dibujar la circunferencia de radio b y centro C que corta la recta r en A.
Dibujar la mediatriz al segmento ![]() que corta la recta CB en el punto B.
que corta la recta CB en el punto B.
Dibujar el triángulo ![]()
Dibujar ![]() .
.
Dibujar la mediatriz al segmento ![]() que corta la recta CB en el punto B’.
que corta la recta CB en el punto B’.
Dibujar el triángulo ![]() .
.
Método 2:
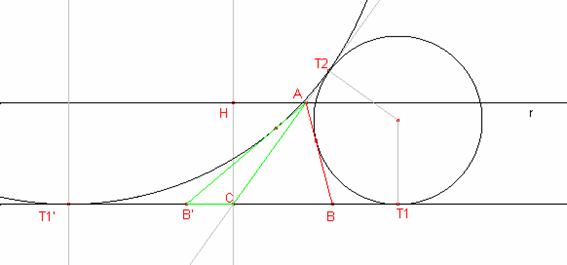
Dibujar ![]() .
.
Dibujar una recta r paralela a CD a una distancia ![]() .
.
Dibujar la circunferencia de radio b y centro C que corta la recta r en A.
Dibujar la recta CA.
La circunferencia de centro C y radio a+b+c corta la recta CA en el punto ![]() .
.
Dibujar la recta perpendicular a ![]() que pasa por
que pasa por ![]()
Dibujar la recta perpendicular a ![]() que pasa por
que pasa por ![]()
Las dos rectas se intersectan en el exincentro del triángulo ![]() .
.
Dibujar la circunferencia exincrita.
Dibujar la recta tangente a la circunferencia exincrita que pasa por A que corta la recta ![]() en el punto B.
en el punto B.
Dibujar el triángulo ![]()
Dibujar ![]() .
.
Dibujar la recta perpendicular a ![]() que pasa por
que pasa por ![]()
Dibujar la circunferencia exincrita.
Dibujar la recta tangente a la circunferencia exincrita que pasa por A que corta la recta ![]() en el punto B’.
en el punto B’.
Dibujar el triángulo ![]() .
.
Ejemplo particular resuelto analíticamente:
Resolver el triángulo ![]() conocidos
conocidos ![]() ,
, ![]() ,
, ![]() .
.
Solución:
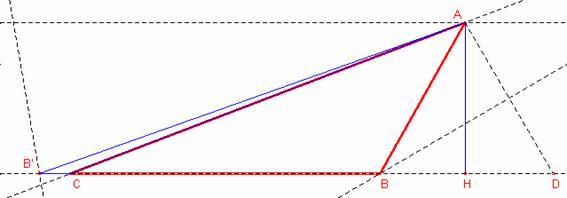 Sea
Sea ![]() altura del triángulo.
altura del triángulo.
Aplicando razones trigonométricas al triángulo rectángulo ![]() :
:
![]() , entonces:
, entonces: ![]() .
.
Supongamos que ![]() .
. ![]() .
.
Aplicando el teorema del coseno al triángulo ![]() :
: ![]() .
.
Consideremos el sistema ![]() su solución es:
su solución es:
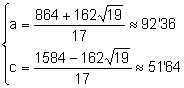 . Teniendo en cuenta que
. Teniendo en cuenta que ![]() B es un ángulo obtuso.
B es un ángulo obtuso.
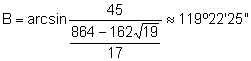 (ángulo obtuso).
(ángulo obtuso). ![]() .
.
Supongamos que ![]() .
. ![]() .análogamente
.análogamente
 . Teniendo en cuenta que
. Teniendo en cuenta que ![]() el ángulo B es agudo.
el ángulo B es agudo.
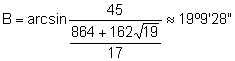 (ángulo agudo).
(ángulo agudo).
![]() .
.