Problema 620

Dado un triángulo ABC, encontrar E sobre la recta BC, F sobre AC y G sobre AB, de manera que

AC² + CE² = AB² +BE²

BA² + AF² = BC² + CF²

CA² + AG² = CB² + BG²

Demostrar que las cevianas AE, BF y CG concurren.

Barroso, R. (2011). Comunicación personal.

Solución del director.

Sea AC=b, CE=m, AB=c, BE=n.

Sea b²+m²=c²+n²

Es b²-n²=c²-m²

Sea b²-n²=c²-m² =j²

Es decir b²=j²+n², y c²=j²+m².

Así, en el caso del acutángulo n y m son los segmentos en que la altura divide al lado a.

Luego E es el simétrico del pie de la altura H_a sobre A respecto al punto medio M_a. Siendo CE=BH_a=m, BE=CH_a=n

De igual manera, F, AF=CH_b=p, CF=AH_b=q

y G, cumple que BG=AH_c=r, AG=BH_c=s.

Dado que AH_a, BH_b y CH_c concurren en H, ortocentro de ABC, es

M p r=n q s, y cqd, AE, BF y CG concurren.

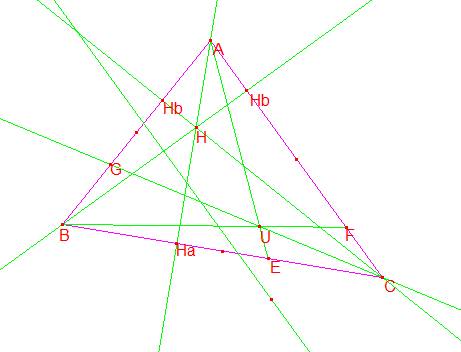
En el caso del triángulo rectángulo en A, F=C, G=B, y G es el simétrico de H_a según M_a y es el punto de concurrencia.

En el caso del triángulo obtusángulo en A, E es interior a BC y G y F son exteriores a AB y AC, y AE, BF y CG concurren fuera del triángulo.

El punto de concurrencia U es el X(69) de la enciclopedia de Kimberling.

http://faculty.evansville.edu/ck6/encyclopedia/ETC.html

Ricardo Barroso Campos.

Didáctica de las Matemáticas.

Universidad de Sevilla.