Problema 620

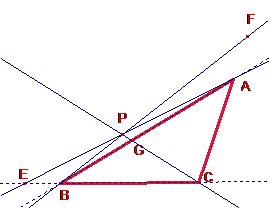
Dado un triángulo , encontrar E sobre la recta BC, F sobre AC y G sobre AB, de manera que:

.

.

.

Demostrar que las cevianas AE, BF y CF concurren

Solución Ricard Peiró:

.

.

.

.

.

Resolviendo la ecuación:

, .

Análogamente,

, .

, .

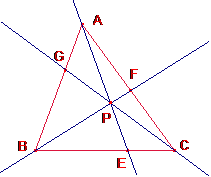
Veamos que las tres cevianas se intersectan en un punto, aplicando el teorema de Ceva:

.

Nota:

Si el triángulo es acutángulo

Los puntos E, F, G son de los lados del triángulo.

Si el triángulo es rectángulo .

Entonces, , , .

Si el triángulo es obtusángulo .

Los puntos E, F son exteriores al triángulo.