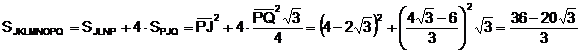Problema 625

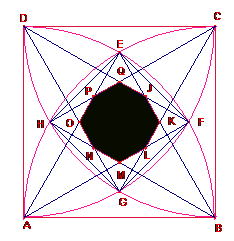Siga ABCD un quadrat de costat 2.

Construïm quatre quadrants de circumferència de centre cadascun dels vèrtexs i radi del costat del quadrat. Els arcs es tallen en els punts E, F, G, H.

Construïm els triangles , , i . Aquests quatre triangles formen un octògon JKLMNOPQ, l’àrea del qual es demana.

Trigueros, R. (2011): Comunicación personal. 

Solució de Ricard Peiró:

, .

Aleshores, .

, aleshores, .

Els triangles , , , són isòsceles i iguals.

L’octògon JKLMNOPQ té tots els costats iguals.

.

Aleshores,

L’àrea de l’octògon és igual a l’àrea del quadrat JLNP de costat més l’àrea de 4 triangles equilàters de costat i altura .

Siga U el centre del quadrat ABCD.

.

.

Aplicant raons trigonomètriques al triangle rectangle :

.

.

.

. Aleshores, .

L’àrea de l’octògon és: