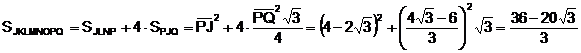Problema 625

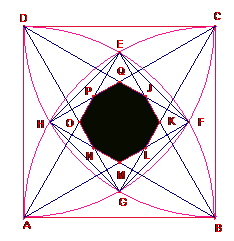
Sea ABCD un cuadrado de lado 2.

Construimos cuatro cuadrantes de circunferencia de centro cada uno de los vértices y radio del lado del cuadrado. Los arcos se cortan en los puntos E, F, G, H.

Construimos los triángulos , , y . Estos cuatro triángulos forman un octógono JKLMNOPQ, cuya área se pide.

Trigueros, R. (2011): Comunicación personal. 

Solución de Ricard Peiró:

, .

Entonces, .

, entonces, .

Los triángulos , , , son isósceles e iguales.

El octógono JKLMNOPQ tiene todos los lados iguales.

.

Entonces,

El área del octógono es igual al área del cuadrado JLNP de lado más el área de 4 triángulos equiláteros de lado y altura .

Sea U el centro del cuadrado ABCD.

.

.

Aplicando razones trigonométricas al triángulo rectángulo :

.

.

.

. Entonces, .

El área del octógono es: