Propuesto
por Ramón Trigueros Reina, profesor Doctor, Asociado del Departamento de
Didáctica de las Matemáticas de la Universidad de Sevilla.
Problema
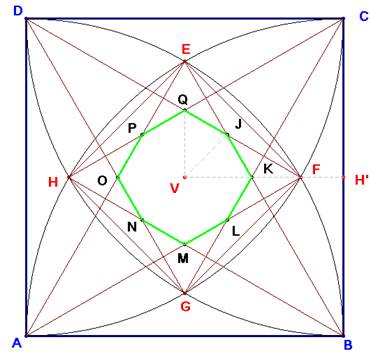
625.- Sea ABCD un cuadrado de lado 2.
Construyamos los cuatro cuadrantes de
circunferencia interiores de centro en cada vértice y radio el lado del cuadrado.
Se cortarán en cuatro puntos
interiores, E F G H
Construyamos los triángulos AFE, BEH, CHG y
DGF.
Estos cuatro triángulos dan lugar a un
octógono común JKLMNOPQ, cuya área se pide.
Trigueros,
R. (2011): Comunicación personal.
Nota: La
construcción aparece en portada del libro "Matemáticas Específicas para
Maestros" de los profesores A. Ariza, R. Trigueros y A. Sánchez.
Solución de Saturnino Campo, profesor del
I.E.S. Fray Luis de León de Salamanca.
En la figura construida es fácil demostrar que el cuadrilátero ALCP es un rombo. Es fácil ver que en cada ángulo del cuadrado concurren segmentos que lo dividen en tres iguales de 30º. De ahí se deduce de inmediato que el polígono en cuestión es un paralelogramo.
De la observación sobre la medida de los ángulos que concurren en los vértices A y C se deduce que el triángulo ALC es isósceles y por tanto el paralelogramo es un rombo (y sus diagonales son perpendiculares). Análogo razonamiento nos sirve para concluir que también es un rombo el cuadrilátero DJBN. Además, los vértices L y P, J y N se encuentran en cada una de las diagonales del cuadrado.
También se deduce que AF (HC) y EB
son perpendiculares. Y también BH y CG, (M
es el baricentro del triángulo equilátero ABE,
K el
del también equilátero CHB). De aquí el ángulo L del
octógono mide 150º, como suplementario de 
.
En el triángulo isósceles CKB, el
ángulo desigual es el ángulo K del
octógono: su medida es de 120º.
Por la simetría de la
figura se van sucediendo en el octógono los ángulos de 150º y 120º de forma
alterna. Para calcular su área bastará con multiplicar por 8 la de uno de los 8
triángulos iguales que se forman desde el centro V del cuadrado (y del octógono).
El área del triángulo VJK es: [VJK] =
.
De la semejanza de los triángulos VJK y AJB
y del teorema de los senos se deduce 
.
Para el área 
del
octógono tendremos:
=
=
.
Queda por calcular 
Como K
es el ortocentro de CHB se tiene KH’ = 
HH’=
,
siendo 
el lado del cuadrado.
.
Finalmente 
= 
=
.
En particular si el
lado mide 2, el valor del área es 
0,45299…
Nota.- El octógono que nos ocupa tiene todos
sus lados iguales, basta observar que L es
el ortocentro del triángulo isósceles BKM
y por tanto, BL es perpendicular a MK de donde resulta que éste último es
paralelo a AC y con ello MLK y ALC son semejantes: ML = LK.
Efectuando un giro de 90º con centro en V
probamos que 
MLK
KJQ. No es un polígono
regular pues sus ángulos interiores no son iguales.