Propuesto por  Julio A.  Miranda Ubaldo. Profesor de I.E.P “San Francisco de Asís”. (Huaral), de Perú.

Problema 626

En la siguiente figura, calcular el valor de “x”

                          

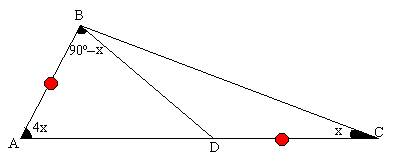
Triángulo ABC, con D sobre el interior de AC, AB=DC, <BAC=4 <BCA, <ABD=90- <BCA.

Origen desconocido

Solución del director.

Sea E el punto de corte de la recta BD con la circunferencia circunscrita a ABC.

<BCE=<BCD+<DCE=x+(90º-x)=90º, por lo que BE es diámetro.

Dado que <CBD=90º-4x >0º, 2x<45º, por lo que el centro O de la circunferencia ha de estar en el segmento BD.

Tracemos el simétrico de la figura completa respecto a O.

C-> C’,  A->  A’,  B-> B’ = E, D-> D’.

Dado que los triángulos DEC y D’BC’ tienen DC=D’C’, DE`=D’B, <CDE=90º-3x=<C’D’B, es <DCE=90º-x=<D’C’B,  y <CEB=4x=D’BC’.

Así CEC’B es rectángulo.  De igual manera A’ C A C’ es rectángulo  

Además AEA’ B también es rectángulo. Por ello, el diámetro COC’ es paralela media y perpendicular a BA. Es decir, el triángulo ACB es en definitiva isósceles,

Por ello, <BAC=4x, <CAB=4x, <ACB=4x, 9x=180º, y por último, x=20º.

Ricardo Barroso Campos.

Didáctica de las Matemáticas.

Universidad de Sevilla.