Propuesto por Julio A. Miranda Ubaldo. Profesor de I.E.P “San Francisco de Asís”. (Huaral), de Perú.
Problema 626
En la siguiente figura, calcular el valor de “x”
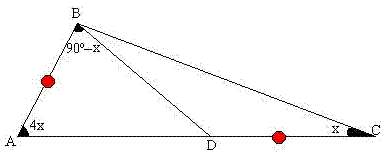
Triángulo ABC, con D sobre el interior de AC, AB=DC, <BAC=4 <BCA, <ABD=90- <BCA.
Origen desconocido
Solución de Milton Favio Donaire Peña (Lima Perú)
Construimos el triángulo APB congruente al triángulo DBC.
El triángulo CBP resulta isósceles, de donde m<ACP=2x
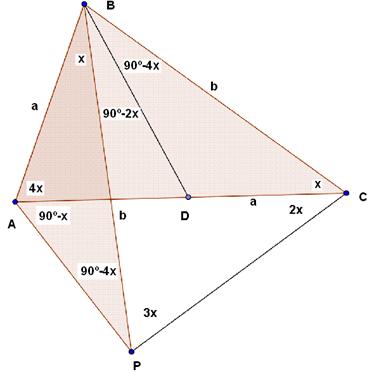
Llenando las medidas angulares , tenemos CA=CP, y como
m<ACP=2 m<ABP , entonces C es el circuncentro del triángulo PAB.
De allí, CB=CA=CP.
Finalmente el triángulo CBP es equilátero. De donde x=20º.