Problema 635.
Cuestiones para resolver:
XXI Demostrar que el área de un triángulo es igual al producto del radio de la circunferencia circunscrita por el semiperímetro del triángulo órtico.
(Nota del director: La propiedad es correcta en el caso de ser el triángulo acutángulo o rectángulo(en este caso el triángulo órtico degenera))
Guiu, M. y Páez, F. (1935): Exposición didáctica de cuestiones geométricas destinada a facilitar la preparación para concursos de ingreso en Academias y Escuelas de carreras científicas. Tomo I 1º Edición. Barcelona
Exposición didáctica de cuestiones geométricas destinada a facilitar la preparación para concursos de ingreso en Academias y Escuelas de carreras científicas. Tomo I 1º Edición. Barcelona
Bosch Casa editorial, Apartado 928
En la enseñanza de las matemáticas existe siempre una necesidad bilateral: El profesor, procurando dar firme posesión de las materias que según plan explica, resuelve algunos ejercicios en clase y propone otros al alumno para que este los resuelva…
Esta referencia está tomada de un ejemplar que se conserva en
El director agradece a
Solución del director.
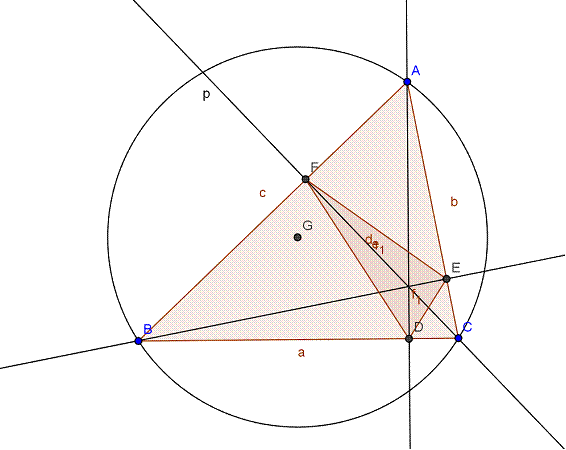
Sea ABC el triángulo acutángulo. Sean D, E y F los pies de las alturas de los vértices A, B y C.
Los triángulos ADC y ADB son rectángulos con AD común. Sea CD=m, DB=a-m
Es AD2=AC2-CD2, por lo que es AD2=b2-m2 , y
también es AD2=AB2-BD2, es decir, AD2=c2-(a-m)2=c2-a2+2am-m2.
Así es b2-m2= c2-a2+2am-m2.
De donde ![]()
Y ![]()
De manera análoga, es ![]()
Y así es: es ![]()
<AEF=180-<FEC=<ABC, por ser el cuadrilátero AEFB inscrito en una circunferencia, por lo que el triángulo AEF es semejante al ABC, por lo que tenemos que:
Al ser AE/AB=AF/AC=EF/BC, es
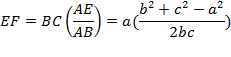
Análogamente, será:
![]() ,
,
Así el semiperímetro de DEF es:
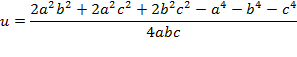
Por otra parte busquemos el valor de R, radio de la circunferencia circunscrita, en función de los lados a,b y c.
Por Herón tenemos que siendo S el área de ABC y p el semiperímetro de ABC, es
![]()
Por otra parte, se tiene
S= (a ha)/2.
Si trazamos el pie de la altura Ha sobre el lado a y el diámetro AA*, los triángulos AHaB
y ACA* son semejantes, y por ello ha/c=b/2R, de donde ha=(cb)/2R.
Por ello es S=abc/4R.
De las tres fórmulas se tiene que:
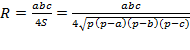
De esta manera tenemos que
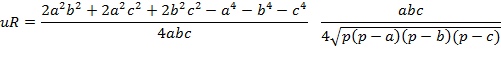
Es decir
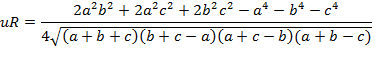
O
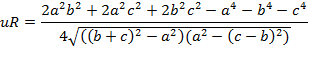
O
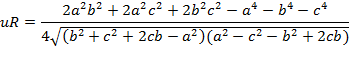
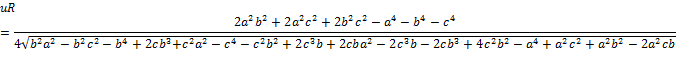
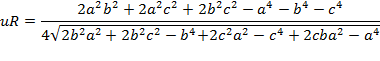
Es decir:
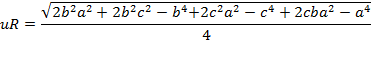
O bien
![]() ,
cqd.
,
cqd.
Si el triángulo es rectángulo con hipotenusa AC,
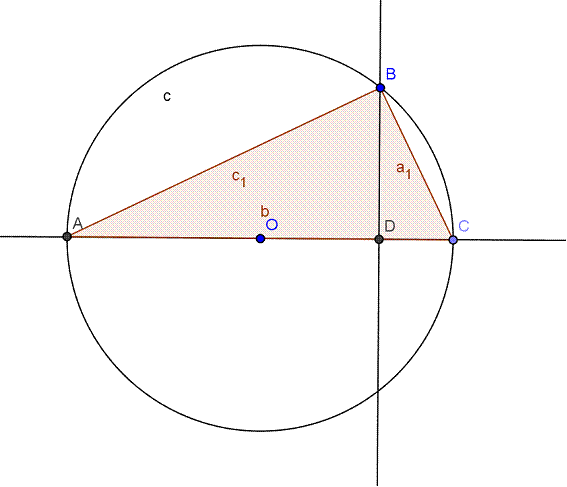
el triángulo órtico degenera en BDB, doble de la altura de B, por lo que su semiperímetro es BD, y el radio de la circunscrita es OC, mitad de la base.
Así, S=(DB)R, cqd.
Ricardo Barroso Campos
Didáctica de las Matemáticas
Universidad de Sevilla.