Problema 636

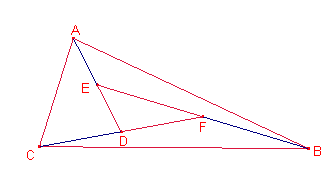
Donat un triangle , determineu dos triangles i tal que el simetric de D respecte de E siga A, el simètric de E respecte de F siga B i el simètric de F respecte de D siga C i que el simètric de G respecte de H siga A, el simètric de H respecte de I siga C i el simètric de I respecte de G siga B.

Determineu els costats dels triangles i en funció de A, b, i c, costats del triangle .

Barroso, R (2012): Comunicación personal.

Solució:

Siga , , .

Siga , , .

Aplicant el teorema del cosinus al triangle :

.

Aplicant el teorema del cosinus al triangle

. Simplificant:

.

Anàlogament:

.

.

Resolent el sistema:

.

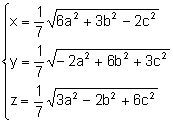Vegem que el problema té solució:

Per la desigualtat triangular:

, elevant al quadrat:

.

(1)

Aplicant la desigualtat entre la mitjana aritmètica i la geomètrica:

(2)

Sumant les expressions (1) (2):

.

Anàlogament:

, .

Vegem que .

Aquesta desigualtat s’assoleix si:

.

Elevant al quadrat:

Elevant al quadrat:

.

Factoritzant l’expressió:

Aquesta desigualtat si que s’assoleix.

Anàlogament, , .

Siga , , .

Siga , , .

Aplicant el teorema del cosinus al triangle :

.

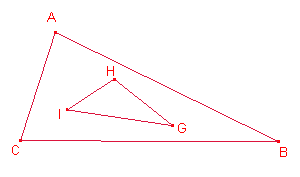Aplicant el teorema del cosinus al triangle

. Simplificant:

.

Anàlogament:

.

.

Resolent el sistema:

.
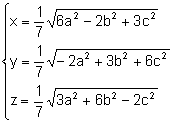