Problema 636

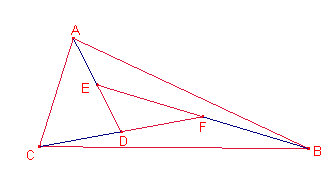
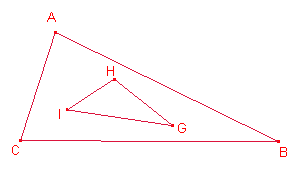
Dado un triángulo , hallar dos triángulos y tales que el simétrico de D respecto a E sea A, el simétrico de E respecto de F sea B y el simétrico de F respecto de D sea C y que el simétrico de G respecto a H sea A, el simétrico de H respecto de I sea C y el simétrico de I respecto de G sea B. Hallar los lados de los dos triángulos y en función de a, b y c, lados de

Barroso, R (2012): Comunicación personal.

Dedicado a mi compañero y amigo José Real Anguas. In memoriam

Solución de Ricard Peiró:

Sea , , .

Sea , , .

Aplicando el teorema del coseno al triángulo :

.

Aplicando el teorema del coseno al triángulo

. Simplificando:

.

Análogamente:

.

.

Resolviendo el sistema:

.

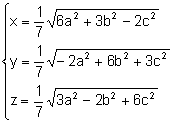Veamos que el problema tiene solución:

Por la desigualdad triangular:

, elevando al cuadrado:

.

(1)

Aplicando la desigualdad entre la media aritmética y la geométrica:

(2)

Sumando las expresiones (1) (2):

.

Análogamente:

, .

Veamos que .

Esta desigualdad se alcanza si:

.

Elevando al cuadrado:

Elevando al cuadrado:

.

Factorizando la expresión:

Esta desigualdad si que es cierta.

Análogamente, , .

Sea , , .

Sea , , .

Aplicando el teorema del coseno al triángulo :

.

Aplicando el teorema del coseno al triángulo

. Simplificando:

.

Análogamente:

.

.

Resolviendo el sistema:

.
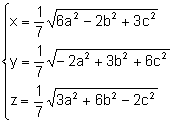