Problema 639

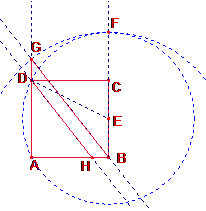
Siga un quadrat ABCD. Siga E el punt mig de .

Tracem la circumferència de centre E i radi  que talla la semirecta BC prolongada per C en el punt F. Tracem la circumferència de centre B i radi . Talla la semirecta AD prolongada per De en el punt G.

El triangle  s’anomena de Kepler.

Determineu la relació amb el nombre d’or.

Tracem per D una paral·lela al segment  que talla el segment  en el punt H.

Demostreu que els triangles ,  tenen cinc elements iguals (tres angles i dos costats).

Askew, M. y Ebbutt, S. (2010): Petit Précis de Géométrie à déguster. (pur les curieux qui voulent tout comprendre) De Pythagorea la conquête spatiale : l'ABC dela Géométrie.  Belin (p. 67, ligeramente adaptada)

Solució de Ricard Peiró i Estruch:

Siga el nombre d’or , solució positiva de l’equació .

Aleshores, .

Siga  costat del quadrat.

Aplicant el teorema de Pitàgores al triangle rectangle :

. .

Aplicant el teorema de Pitàgores al triangle :

.

Aleshores, els costats del triangle  estan en progressió geomètrica de raó .

Els triangles rectangles ,  són semblants, aleshores, tenen els angles iguals i els costats proporcionals:

.  .

.

Aleshores, els triangles ,  tenen cinc elements iguals (tres angles i dos costats).