Problema 639

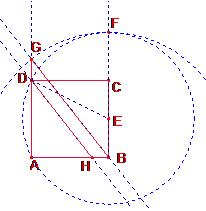
Sea un cuadrado ABCD.  Sea E el punto medio de BC. Tracemos la circunferencia de centro E y radio ED. Cortará a la semirrecta BC prolongada por C en F. Tracemos la circunferencia de centro B  y radio BF. Cortará a la semirrecta AD prolongada  por D en G. El triángulo ABG se denomina de Kepler.  Hallar la relación con el número de oro.

Tracemos por D una paralela a GB que cortará al segmento AB en H. Demostrar que los triángulos ABG y AHD tienen cinco elementos iguales (tres ángulos y dos lados).

Askew, M. y Ebbutt, S. (2010): Petit Précis de Géométrie à déguster. (pur les curieux qui voulent tout comprendre) De Pythagorea la conquête spatiale : l'ABC dela Géométrie.  Belin (p. 67, ligeramente adaptada)

Solución de Ricard Peiró i Estruch:

Sea el número de oro , solución positiva de la ecuación .

Entonces, .

Sea  lado del cuadrado.

Aplicando el teorema de Pitágoras al triángulo rectángulo :

.

.

Aplicando el teorema de Pitágoras al triángulo :

.

Entonces, los lados del triángulo  están en progresión geométrica de razón .

Los triángulos rectángulos ,  son semejantes, entonces, tienen los ángulos iguales y los lados proporcionales:

.  .

.

Entonces, los triángulos ,  tienen cinco elementos iguales (tres ángulos y dos lados).