Problema 639 de triánguloscabri:

Sea un cuadrado ABCD.  Sea E el punto medio de BC. Tracemos la circunferencia de centro E y radio ED. Cortará a la semirrecta BC prolongada por C en F. Tracemos la circunferencia de centro B  y radio BF. Cortará a la semirrecta AD prolongada  por D en G. El triángulo ABG se denomina de Kepler.  Hallar la relación con el número de oro.

Tracemos por D una paralela a GB que cortará al segmento AB en H. Demostrar que los triángulos ABG y AHD tienen cinco elementos iguales (tres ángulos y dos lados).

Askew, M. y Ebbutt, S. (2010): Petit Précis de Géométrie à déguster. (pur les curieux qui voulent tout comprendre) De Pythagorea la conquête spatiale : l'ABC dela Géométrie.  Belin (p. 67, ligeramente adaptada)

).

Solución de Víctor Cabezas, estudiante de 4º de ESO, en el IES Maestro Juan de Ávila (Ciudad Real)

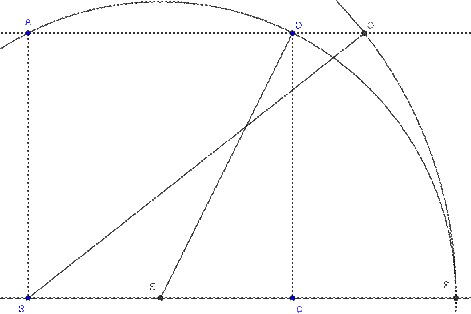
Hagamos, sin pérdida de generalidad,  BC=1, entonces, aplicando el teorema de Pitágoras al ∆ EDC, el segmento ED=. Y por definición de F, ED=EF. Por lo que

BF=  =BG=φ

Como del ∆ ABG, rectángulo en A, conocemos dos lados, podemos conocer el tercero. Así AG= φ.

De donde se concluye que los lados del ∆ ABG están en progresión geométrica de razón  .

 

Tracemos por D una paralela a GB que cortará al segmento AB en H. Demostrar que los triángulos ABG y AHD tienen cinco elementos iguales (tres ángulos y dos lados).

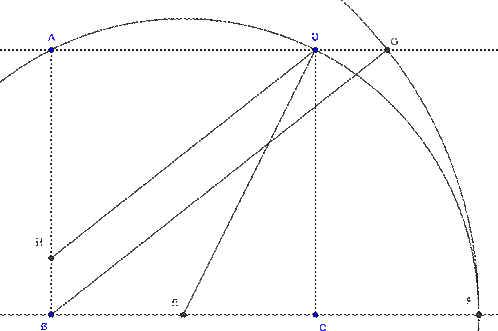
Por semejanza de ∆ ABG y ∆ AHD los ángulos serán iguales.

Por otro lado el lado AD=AB y como  DH==AG.

Por lo que ambos triángulos tienen cinco elementos iguales .