Propuesto por Juan Bosco Romero Márquez, profesor colaborador de
Problema 642
Dado ABC un triángulo, AD una ceviana arbitraria, y se toman los puntos E, F sobre los lados AC y AB respectivamente de forma que: las rectas AD, BE, CF se cortan en A´,
y los triángulos CFH y BEG, son rectángulos en E y en F, y los puntos D, G, y H, están en BC.
Definimos los puntos: I= DF y BE y J=ED y CF, L= AJ y BC, M=AI y BC
Probar si es cierto o no que:
a1) Las rectas AD , BJ y CI concurren en un punto que denotamos por K.
a2) Las rectas AD, LF y EM se cortan en K.
b) Lugar geométrico de los puntos K, cuando AD varía.
c) Razón doble de los puntos A, A´, K, D.
Romero, J.B. (2012): Comunicación personal.
Resuelto por JULIÁN SANTAMARÍA TOBAR profesor de Dibujo del IES
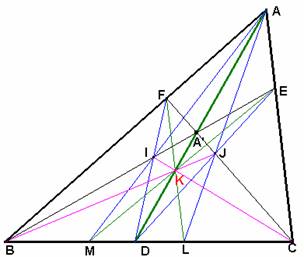 Cuando la razón doble de cuatro puntos tiene un valor de -1 se denomina Cuaterna Armónica. Una de las propiedades del cuadrilátero completo es que cada diagonal queda dividida armónicamente por las otras dos. Veamos en la figura el cuadrilátero I K A’ F que al alargar los lados nos dan otros dos vértices el D y el C, y esta diagonal DC es cortada por las otras dos diagonales en B y L por lo tanto se puede afirmar que la cuaterna (BLDC) es armónica. Como las razones dobles son invariantes proyectivas, al proyectar desde A (BLDC) resulta que (FJA’C) es armónica, y al volver a proyectar (FJA’C) desde B resulta que (AKA’D) también forman una cuaterna armónica. A esta concusión se puede llagar del mismo modo partiendo del cuadrilátero JKA’E.
Cuando la razón doble de cuatro puntos tiene un valor de -1 se denomina Cuaterna Armónica. Una de las propiedades del cuadrilátero completo es que cada diagonal queda dividida armónicamente por las otras dos. Veamos en la figura el cuadrilátero I K A’ F que al alargar los lados nos dan otros dos vértices el D y el C, y esta diagonal DC es cortada por las otras dos diagonales en B y L por lo tanto se puede afirmar que la cuaterna (BLDC) es armónica. Como las razones dobles son invariantes proyectivas, al proyectar desde A (BLDC) resulta que (FJA’C) es armónica, y al volver a proyectar (FJA’C) desde B resulta que (AKA’D) también forman una cuaterna armónica. A esta concusión se puede llagar del mismo modo partiendo del cuadrilátero JKA’E.
Por lo tanto se puede probar:
a) Si se toma un punto cualquiera A’ en la ceviana DA el punto K será un punto único por formar (AKA’D) una cuaterna armónica
b) Si se deslizara el punto D sobre el segmento BC y la razón simple AA’D se mantiene, el punto K describe un segmento paralelo a BC por mantener constante la otra razón simple AKD
c) La razón doble de los puntos A, A’ K, D, aunque se pueden ordenar de 4! = 24 modos, es habitual ordenar estos cuatro puntos o expresar esta razón doble de este modo: (AKA’D) cuyo valor es -1